Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Neperiano » Sex Out 10, 2008 22:22
por Neperiano » Sex Out 10, 2008 22:22
Eu acho esses exercícios muito fáceis, mas de qualquer forma coloquei eles em médios, e para deixar eles mais dificies, eu vou colocar mais de um, e vou cobrar toda a resolução dos problemas abaixo.
1) Se você multiplicar um número real x por ele mesmo e do resultado subtrair 14, você vai obter o quíntuplo do número x. Qual é esse número?
2) Determine um número real "a" para que as expressões (3a + 6)/ 8 e (2a + 10)/6 sejam iguais.
3)O número -3 é a raíz da equação x2 - 7x - 2c = 0. Nessas condições, determine o valor do coeficiente c?
4) Resolver as seguintes equações (na incógnita x):
a) 5/x - 2 = 1/4 (x diferente de 0)
b) 3bx + 6bc = 7bx + 3bc
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sex Out 10, 2008 22:44
por Molina » Sex Out 10, 2008 22:44
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sex Out 10, 2008 22:46
por Molina » Sex Out 10, 2008 22:46
Agora que li que era pra outras pessoas resolverem.
Desculpa. Nao resolvo as outras

(Só se ninguem fizer)
Abraços.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Sáb Out 11, 2008 10:40
por Neperiano » Sáb Out 11, 2008 10:40
Não é isso Molina, na verdade é que não tem graça vc responder, vc vai acertar sempre, dai ja aparece a resposta, então assim vc pode resolver mas não coloca a resposta, a menos q vc naum saiba, mas se souber, fala comigo pelo chat e pergunta.
A sua resposta esta correta.
Abraços
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por DanielFerreira » Dom Jul 26, 2009 12:45
por DanielFerreira » Dom Jul 26, 2009 12:45
Maligno escreveu:2) Determine um número real "a" para que as expressões (3a + 6)/ 8 e (2a + 10)/6 sejam iguais.

18a + 36 = 16a + 80
18a - 16a = 80 - 36
2a = 44
a = 22"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Dom Jul 26, 2009 12:48
por DanielFerreira » Dom Jul 26, 2009 12:48
Maligno escreveu:3)O número -3 é a raíz da equação x2 - 7x - 2c = 0. Nessas condições, determine o valor do coeficiente c?
x² - 7x - 2c = 0
(- 3)² - 7 * (- 3) - 2c = 0
9 + 21 = 2c
2c = 30
c = 15"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Dom Jul 26, 2009 12:52
por DanielFerreira » Dom Jul 26, 2009 12:52
Maligno escreveu:4) Resolver as seguintes equações (na incógnita x):
a) 5/x - 2 = 1/4 (x diferente de 0)

4 * 5 - 2 * 4x = 1 * x
20 - 8x = x
20 = 9x
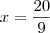
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Dom Jul 26, 2009 12:55
por DanielFerreira » Dom Jul 26, 2009 12:55
Maligno escreveu:4) Resolver as seguintes equações (na incógnita x):
b) 3bx + 6bc = 7bx + 3bc
6bc - 3bc = 7bx - 3bx
4bx = 3bc
4x = 3c
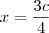
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equações de 2º grau
por Lismara » Seg Ago 31, 2009 23:25
- 4 Respostas
- 2841 Exibições
- Última mensagem por Lismara

Ter Set 01, 2009 21:42
Sistemas de Equações
-
- Equações 2º Grau
por Quatroemes » Dom Mar 21, 2010 20:53
- 2 Respostas
- 2617 Exibições
- Última mensagem por Quatroemes

Seg Mar 22, 2010 11:34
Funções
-
- equacoes do 2 Grau
por guillcn » Qui Jun 30, 2011 12:30
- 1 Respostas
- 1595 Exibições
- Última mensagem por joaofonseca

Qui Jun 30, 2011 15:25
Equações
-
- equaçoes do 1 grau
por thalia alexandrina » Seg Out 10, 2011 14:29
- 3 Respostas
- 3007 Exibições
- Última mensagem por MarceloFantini

Ter Out 11, 2011 23:06
Sistemas de Equações
-
- Equações do 3º grau
por baianinha » Qua Mar 14, 2012 16:09
- 3 Respostas
- 2254 Exibições
- Última mensagem por nicolegcg

Ter Jun 12, 2012 14:47
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


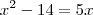


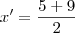





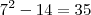







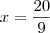
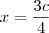


 , avisa que eu resolvo.
, avisa que eu resolvo.

