 por CarolMarques » Qui Mai 24, 2012 11:04
por CarolMarques » Qui Mai 24, 2012 11:04
São dados ,em cada caso, o parâmetro geométrico a e os focos de uma hipérbole.Obtenha uma equação algébrica de segunda grau em x e y que todo ponto(x,y,) da hipérbole deva satisfazer.
a=1; F1=(3,4); F2=(-1,-2)
Eu percebi que a hipérbole deve possuir na equação um termo quadrado misto(Bxy) mas não sei como usar os conceitos de rotação e translação dos eixos para achar a equação.Eu só consigo fazer o inverso.Por favor me ajudem.
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por LuizAquino » Sáb Mai 26, 2012 19:08
por LuizAquino » Sáb Mai 26, 2012 19:08
CarolMarques escreveu:São dados ,em cada caso, o parâmetro geométrico a e os focos de uma hipérbole.Obtenha uma equação algébrica de segunda grau em x e y que todo ponto(x,y,) da hipérbole deva satisfazer.
a=1; F1=(3,4); F2=(-1,-2)
CarolMarques escreveu:Eu percebi que a hipérbole deve possuir na equação um termo quadrado misto(Bxy) mas não sei como usar os conceitos de rotação e translação dos eixos para achar a equação.Eu só consigo fazer o inverso.Por favor me ajudem.
Assim como foi feito em seu outro tópico (
Parábola), a ideia é aplicar a definição da cônica em questão. Nesse caso, a definição da hipérbole.
Sabemos que a hipérbole é o conjunto dos pontos no plano cujo a diferença entre as suas distâncias a dois pontos fixos (chamados de focos) é sempre constante.
Em outras palavras, se P = (x, y) é um ponto dessa hipérbole e F1 e F2 são seus focos, então o valor de |d(P, F1) - d(P, F2)| é sempre constante. Considerando que essa constante seja 2a, temos então que |d(P, F1) - d(P, F2)| = 2a.
Substituindo os dados fornecidos no exercício, temos que:
![\left|\sqrt{(x-3)^2 + (y-4)^2} - \sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right| = 2\cdot 1 \left|\sqrt{(x-3)^2 + (y-4)^2} - \sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right| = 2\cdot 1](/latexrender/pictures/fb94b03c71a95f9a93234e5cb943085f.png)
Agora tente concluir o exercício. Se você não conseguir, então poste aqui até onde você conseguiu avançar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por CarolMarques » Sáb Mai 26, 2012 21:11
por CarolMarques » Sáb Mai 26, 2012 21:11
Depois que eu vi a resposta no outro tópico eu até tentei fazer essa mesma questão pela definição , mas eu não consigo eliminar a raiz , eu elevo tudo ao quadradro mas permanece a raiz.Como eu faço pra tirá-la?
-
CarolMarques
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qui Mai 03, 2012 20:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [HIPÉRBOLE] Porque yz = 4 é uma hipérbole??
por Sohrab » Qui Abr 25, 2013 03:41
- 1 Respostas
- 2696 Exibições
- Última mensagem por LuizAquino

Qui Abr 25, 2013 19:17
Geometria Analítica
-
- Hiperbole
por Schimuneck » Seg Mai 30, 2011 10:21
- 1 Respostas
- 5733 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 14:29
Geometria Analítica
-
- [Hipérbole]
por Ana_Rodrigues » Qua Nov 23, 2011 19:33
- 3 Respostas
- 4043 Exibições
- Última mensagem por MarceloFantini

Qua Nov 23, 2011 20:54
Geometria Analítica
-
- Hiperbole
por Claudin » Qui Mai 24, 2012 02:44
- 2 Respostas
- 1940 Exibições
- Última mensagem por Claudin

Ter Jun 12, 2012 20:31
Geometria Analítica
-
- Hiperbole
por Claudin » Qui Mai 24, 2012 02:47
- 2 Respostas
- 1766 Exibições
- Última mensagem por Claudin

Ter Jun 12, 2012 20:32
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\left|\sqrt{(x-3)^2 + (y-4)^2} - \sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right| = 2\cdot 1 \left|\sqrt{(x-3)^2 + (y-4)^2} - \sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right| = 2\cdot 1](/latexrender/pictures/fb94b03c71a95f9a93234e5cb943085f.png)

![\left\{\left|\sqrt{(x-3)^2 + (y-4)^2} - \sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right|\right\}^2 = (2\cdot 1)^2 \left\{\left|\sqrt{(x-3)^2 + (y-4)^2} - \sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right|\right\}^2 = (2\cdot 1)^2](/latexrender/pictures/1ef494255ecb5aa167758026bca39585.png)
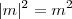 . Sendo assim, podemos retirar o módulo que aparece no primeiro membro deixando apenas a potência 2. Ficamos então com:
. Sendo assim, podemos retirar o módulo que aparece no primeiro membro deixando apenas a potência 2. Ficamos então com:![\left\{\sqrt{(x-3)^2 + (y-4)^2} - \sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right\}^2 = 4 \left\{\sqrt{(x-3)^2 + (y-4)^2} - \sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right\}^2 = 4](/latexrender/pictures/33e91dfce0c4095e9e98d5b323cef656.png)
![\left[\sqrt{(x-3)^2 + (y-4)^2}\left]^2 - 2\sqrt{(x-3)^2 + (y-4)^2}\sqrt{[x-(-1)]^2 + [y-(-2)]^2}\, \left[\sqrt{(x-3)^2 + (y-4)^2}\left]^2 - 2\sqrt{(x-3)^2 + (y-4)^2}\sqrt{[x-(-1)]^2 + [y-(-2)]^2}\,](/latexrender/pictures/b886a1cc3bc5d057b06d47d2f8ab132d.png)
![+ \left\{\sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right\}^2 = 4 + \left\{\sqrt{[x-(-1)]^2 + [y-(-2)]^2}\right\}^2 = 4](/latexrender/pictures/eb3885de94297bfa171e4c281b4192dd.png)

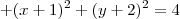
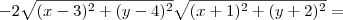

![\left[- 2\sqrt{(x-3)^2 + (y-4)^2}\sqrt{(x+1)^2 + (y+2)^2}\right]^2 =\, \left[- 2\sqrt{(x-3)^2 + (y-4)^2}\sqrt{(x+1)^2 + (y+2)^2}\right]^2 =\,](/latexrender/pictures/53958672e2d85fbfd551b5663abac5c1.png)
![\left[4 - (x-3)^2 - (y-4)^2 - (x+1)^2 - (y+2)^2\right]^2 \left[4 - (x-3)^2 - (y-4)^2 - (x+1)^2 - (y+2)^2\right]^2](/latexrender/pictures/f5afce50999ae4982407be40ad05125d.png)
![4\left[(x-3)^2 + (y-4)^2\right]\left[(x+1)^2 + (y+2)^2}\right] =\, 4\left[(x-3)^2 + (y-4)^2\right]\left[(x+1)^2 + (y+2)^2}\right] =\,](/latexrender/pictures/56385dd3b0f93245cc43eae2a6534270.png)





