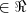 tais que 3x - y = 20. O menor valor de
tais que 3x - y = 20. O menor valor de  é:
é:a) 2
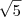
b) 2

c) 2

d) 4
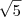
e) 4

Resposta: Alternativa b)
* Bom, aqui está o que eu tentei fazer, mas obviamente não fechou com o resultado:
3x - y = 20
y = 3x - 20;
Substituindo na raiz:



O valor sob a raiz sera o menor possível no vértice da parábola descrita pela função
 , já que o coeficiente de
, já que o coeficiente de  é positivo (ou seja, concavidade pra cima, e valor mínimo).
é positivo (ou seja, concavidade pra cima, e valor mínimo).yv =
 ;
;yv =
 ;
;yv =
 ;
;yv = 4;
Raiz de 4 é 2. Não fecha com nenhuma das alternativas. Alguém pode me indicar o caminho certo? Qual seria o menor valor assumido pelo expressão na raiz?


 , e daí calculei o yv. Não sei porque fiz isso...
, e daí calculei o yv. Não sei porque fiz isso...
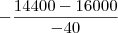

 .
.



