 por ricardosanto » Sex Mai 25, 2012 22:20
por ricardosanto » Sex Mai 25, 2012 22:20
Ola, desejo que alguém analise estas resoluções, para eu saber se estou respondendo certo.
resolvi de acordo com exemplos que vi no livro, e nao sei pq ele não usa o método dos dois caminhos para a resolução.
Se estas respostas estiverem corretas, eu posso afirmar que o limite eh este numero que encontrei? (zero, dois e menos um)
O que a negaçao ( (x\neq y)na A e B e (x\neq 1) na C ) pode afetar na resolução?
A)
![\lim_{(x,y)->(1,1)(x\neq y)} \frac{x^2-2xy+y^2}{x-y}=\lim_{(x,y)->(1,1)} \frac{(x-y)^2}{x-y}= \lim_{(x,y)->(1,1)} \frac{(x-y)*(x-y)}{x-y}=
\lim_{(x,y)->(1,1)} (x-y)=\lim_{(x,y)->(1,1)} (1-1) =zero
[tex] \lim_{(x,y)->(1,1)(x\neq y)} \frac{x^2-2xy+y^2}{x-y}=\lim_{(x,y)->(1,1)} \frac{(x-y)^2}{x-y}= \lim_{(x,y)->(1,1)} \frac{(x-y)*(x-y)}{x-y}=
\lim_{(x,y)->(1,1)} (x-y)=\lim_{(x,y)->(1,1)} (1-1) =zero
[tex]](/latexrender/pictures/4cd2443b58e27bd81b521cddbc0ef07c.png)


B)
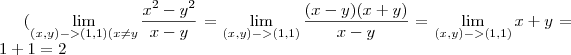

C)

obrigado a quem responder
Editado pela última vez por
ricardosanto em Sáb Mai 26, 2012 13:43, em um total de 1 vez.
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por LuizAquino » Sáb Mai 26, 2012 07:25
por LuizAquino » Sáb Mai 26, 2012 07:25
ricardosanto escreveu:Ola, desejo que alguém analise estas resoluções, para eu saber se estou respondendo certo.
As suas soluções estão corretas.
ricardosanto escreveu:resolvi de acordo com exemplos que vi no livro, e nao sei pq ele não usa o método dos dois caminhos para a resolução.
Porque nesse caso é como se você já tivesse provado, usando todas aquelas considerações sobre os caminhos, que
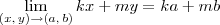
.
Em seguida, você está apenas simplificando todos os limites apresentados para que fiquem nesse formato básico.
ricardosanto escreveu:Se estas respostas estiverem corretas, eu posso afirmar que o limite eh este numero que encontrei? (zero, dois e menos um)
Sim.
ricardosanto escreveu:O que a negaçao (
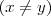
na A e B e

na C ) pode afetar na resolução?
Essas restrições (ou condições de existência) servem para que os limites fiquem bem definidos. No itens A) e B), note que não poderia haver x = y, pois apareceria uma divisão por zero. Já no item c), a divisão por zero apareceria caso x = 1.
Tipicamente, essas restrições não precisam ser ditas de forma explícita no exercício. A pessoa deve ser capaz de olhar para a função dentro do limite e reconhecer essas restrições. Nesse contexto, o método de resolução que você empregou não é afetado por isso.
Editado pela última vez por
LuizAquino em Sáb Mai 26, 2012 18:22, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ricardosanto » Sáb Mai 26, 2012 13:45
por ricardosanto » Sáb Mai 26, 2012 13:45
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite trigonométrico de duas variáveis] Alguém ??
por dwshau » Qui Jun 15, 2017 03:16
- 0 Respostas
- 2795 Exibições
- Última mensagem por dwshau

Qui Jun 15, 2017 03:16
Cálculo: Limites, Derivadas e Integrais
-
- não consigo resolver estas questões
por igorluanabianca » Sex Jul 24, 2009 19:58
- 2 Respostas
- 3789 Exibições
- Última mensagem por Cleyson007

Sáb Jul 25, 2009 09:52
Matemática Financeira
-
- [Sistemas de equações] Como se chegar a estas constantes?
por Wilson de Andrade » Dom Mar 11, 2012 16:08
- 2 Respostas
- 1795 Exibições
- Última mensagem por LuizAquino

Seg Mar 12, 2012 01:23
Funções
-
- quero achar o x do paralelogramo!!
 por ra-phaela » Dom Jul 19, 2009 14:37
por ra-phaela » Dom Jul 19, 2009 14:37
- 2 Respostas
- 2151 Exibições
- Última mensagem por Molina

Dom Jul 19, 2009 16:39
Geometria Espacial
-
- Quero saber dessa integral
por baianinha » Qui Dez 16, 2010 12:35
- 1 Respostas
- 1675 Exibições
- Última mensagem por Moura

Qui Dez 16, 2010 14:08
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{(x,y)->(1,1)(x\neq y)} \frac{x^2-2xy+y^2}{x-y}=\lim_{(x,y)->(1,1)} \frac{(x-y)^2}{x-y}= \lim_{(x,y)->(1,1)} \frac{(x-y)*(x-y)}{x-y}=
\lim_{(x,y)->(1,1)} (x-y)=\lim_{(x,y)->(1,1)} (1-1) =zero
[tex] \lim_{(x,y)->(1,1)(x\neq y)} \frac{x^2-2xy+y^2}{x-y}=\lim_{(x,y)->(1,1)} \frac{(x-y)^2}{x-y}= \lim_{(x,y)->(1,1)} \frac{(x-y)*(x-y)}{x-y}=
\lim_{(x,y)->(1,1)} (x-y)=\lim_{(x,y)->(1,1)} (1-1) =zero
[tex]](/latexrender/pictures/4cd2443b58e27bd81b521cddbc0ef07c.png)


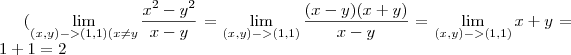




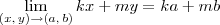 .
.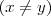 na A e B e
na A e B e  na C ) pode afetar na resolução?
na C ) pode afetar na resolução?


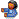


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.