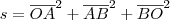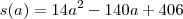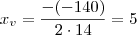Pessoal, estou com dificuldades para entender o enunciado... segue o exercício!
Entre os triângulos OAB com o vértice O na origem e os outros dois vértices A e B, respectivamente, nas retas y =1 e y =3 e alinhados com o ponto P(7,0), determine aquele para o qual é mínima a soma dos quadrados dos lados.
Mas por que ''os triângulos OAB''? ''determine aquele (seria aquele triangulo para o qual é mínima a soma dos quadrados dos lados?)
Quem puder me explicar e me dar idéia sobre qual caminho seguir eu agradeço!