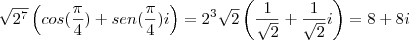por alentejana » Ter Mai 22, 2012 16:40
por alentejana » Ter Mai 22, 2012 16:40
faltou ali o parentesis no i^2:
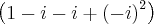
-
alentejana
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 22, 2012 15:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: formado
 por Cleyson007 » Ter Mai 22, 2012 17:33
por Cleyson007 » Ter Mai 22, 2012 17:33
Boa tarde Alantejana!
O procedimento que você adotou não é o ideal para resolver esse tipo de exercício. Imagine se tivessémos uma potência 35, por exemplo, você iria repetir isso 35 vezes?
Analisando sua resolução:
Repare um erro logo no início (2ª linha): (1 - i)(1 - i) --> 1 -i -i
+i² =
1 - 2i + i² Outra coisa: você postou uma segunda mensagem para informar que faltou um parêntese. Quando for assim, clique no botão editar que você consegue alterar por lá, ok?
Alantejana, tente dar sequência no exercício e comente qualquer dúvida

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por alentejana » Ter Mai 22, 2012 17:35
por alentejana » Ter Mai 22, 2012 17:35
"Repare um erro logo no início (2ª linha): (1 - i)(1 - i) --> 1 -i -i +i² = 1 - 2i + i² "
Mas ao fazer

isso fica na mesma 1-2i-1 que dá -2i....
Acho que não percebi...
-
alentejana
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 22, 2012 15:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: formado
 por alentejana » Ter Mai 22, 2012 19:57
por alentejana » Ter Mai 22, 2012 19:57
OK, tentei agora pelo método do Binómio de Newton... mas o resultado deu o mesmo. Onde estou a errar?
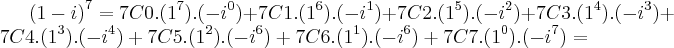
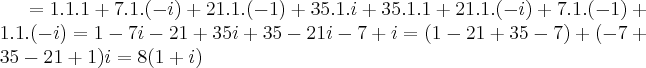
Novamente o resultado é o mesmo. Mas eu estou a fazer:
(-i)^0=1
(-i)^1=(-1)^1 x i^1= -i
(-i)^2=(-1)^2 x i^2= -1
(-i)^3=(-1)^3 x i^3= (-1) x (-i)=i
(-i)^4=(-i)^0= 1
(-i)^5=(-i)^1= -i
(-i)^6=(-i)^2= -1
(-i)^7=(-i)^3= -i
Será que estou a fazer mal por ser (-i)^n em vez de i^n?
-
alentejana
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 22, 2012 15:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: formado
 por alentejana » Ter Mai 22, 2012 20:16
por alentejana » Ter Mai 22, 2012 20:16
Obrigada Cleyson007
O que eu acho é que é mesmo erro do enunciado, pois ele pede para demonstrar a igualdade e 8(1+i) não é igual a -8(1+1). Eu pensei foi que me tivesse enganado nalgum calculo. Agora vou tentar resolver o outro exercicio pelo binomio de newton... Já vai meio caminho andado

Obrigada
-
alentejana
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 22, 2012 15:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: formado
 por joaofonseca » Ter Mai 22, 2012 20:25
por joaofonseca » Ter Mai 22, 2012 20:25
Eu cheguei ao mesmo resultado por duas formas diferentes:
1) Lei Binomial:
Sabemos que

, para qualquer
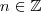
. Sabemos também que

. Podemos então escrever:
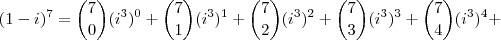
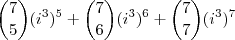

2)Forma Trigonometrica:
Seja

.Então

e

.
Logo
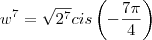
.
Fica:
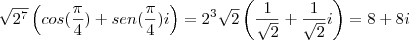
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstrações
por anamendes » Sáb Abr 28, 2012 13:02
- 1 Respostas
- 1209 Exibições
- Última mensagem por LuizAquino

Sáb Abr 28, 2012 14:29
Trigonometria
-
- Demonstrações Duvidas
por Razoli » Qui Ago 08, 2013 22:35
- 1 Respostas
- 1126 Exibições
- Última mensagem por e8group

Sex Ago 09, 2013 10:23
Álgebra Linear
-
- Demonstrações! Álgebra elementar
por Abelardo » Ter Mar 08, 2011 00:42
- 5 Respostas
- 6918 Exibições
- Última mensagem por Abelardo

Ter Mar 08, 2011 14:35
Álgebra Elementar
-
- [Teoria de Grupos] Demonstrações
por Bruna_Ferreira » Seg Jan 05, 2015 16:18
- 1 Respostas
- 1776 Exibições
- Última mensagem por adauto martins

Sex Jan 09, 2015 16:05
Álgebra Elementar
-
- Demonstrações - composta e trigonom etrica
por mathsoliver » Dom Abr 12, 2015 19:07
- 0 Respostas
- 1124 Exibições
- Última mensagem por mathsoliver

Dom Abr 12, 2015 19:07
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.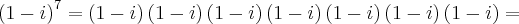
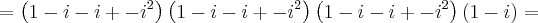
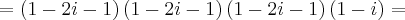
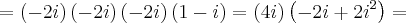


 .
.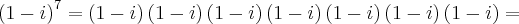
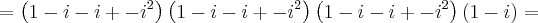
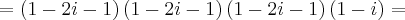
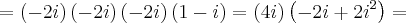


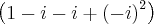





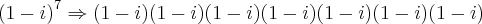


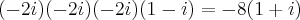
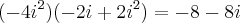
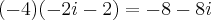
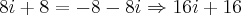


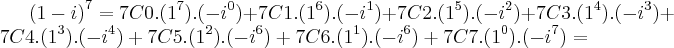
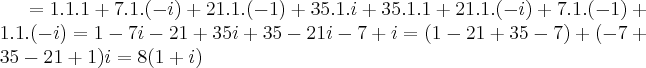



 , para qualquer
, para qualquer 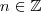 . Sabemos também que
. Sabemos também que  . Podemos então escrever:
. Podemos então escrever: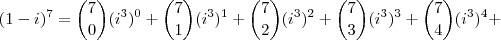
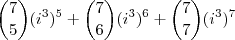

 .Então
.Então  e
e  .
.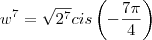 .
.