-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qui Mar 06, 2008 13:12
por admin » Qui Mar 06, 2008 13:12
Olá Ananda, boa tarde!
A região que está em destaque na sua figura, não é a que o enunciado pede a área.
Eu sei que vendo esta equação

logo pensamos em desenvolver a soma de arcos.
Mas, você pensou na solução geral?
Lembra do conjunto-solução de uma equação trigonométrica que comentei na dúvida anterior?
Tente este caminho!
Encontre o conjunto-solução.
Você terá um

inteiro.
Em seguida, veja que o enunciado especifica um intervalo.
Encontre os valores de

que atendem à condição.
Somente então, você poderá extrair duas retas.
Trace as duas retas no plano cartesiano.
A área pedida está entre elas, no primeiro quadrante, e realmente é
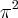
.
Vamos conversando...
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qui Mar 06, 2008 14:17
por admin » Qui Mar 06, 2008 14:17
Ananda, antes, só um comentário.
Eu entendi o que você quis dizer aqui, mas não se deve escrever desta forma:
cos = 0 -->

A idéia fica expressa assim:
Para
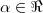
,
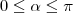
,

Igualmente:
Para

real,
![\alpha \in [0, \pi] \alpha \in [0, \pi]](/latexrender/pictures/0842c803519eb6c851b3f39181776d01.png)
,

Voltando, o conjunto-solução é este mesmo, está certo!
E

ou

, ótimo!
Você precisa sim utilizar os ângulos, mas em radianos, não em graus.
E depois, por favor, comente como você traça retas no plano cartesiano.
Parece ingênuo, mas é importante. Farei novos comentários a partir de sua resposta.
O exercício está quase acabando. Uma vez que você visualizar as retas, será fácil o cálculo da área pedida.
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qui Mar 06, 2008 16:58
por admin » Qui Mar 06, 2008 16:58
Olá!
Certo!
Parece que sua dúvida inicial teve relação com o primeiro quadrante.
Apenas para registrar, sendo
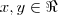
, o primeiro quadrante é a intersecção das regiões representadas por estas inequações:

Veja na figura, incluindo o círculo trigonométrico:

- primeiro_quadrante.jpg (25.97 KiB) Exibido 10121 vezes
E a região do enunciado realmente não cabe dentro do círculo que possui área

.
Sobre os gráficos, seria melhor eu ter perguntado, não como você desenha, mas como você pensa.
No caso de retas, há várias formas, mas acredito que se você fizer uso do que eu tentarei explicar, conseguirá esboçar muitos gráficos mentalmente, apenas olhando para suas equações.
Escrevi um tópico só para o assunto:
Pensando e esboçando gráficoshttp://www.ajudamatematica.com/viewtopic.php?f=72&t=150Bons estudos!
Espero ter ajudado!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Qui Mar 06, 2008 17:48
por Ananda » Qui Mar 06, 2008 17:48
Oi!
É o método da "tabelinha" mesmo...
Mas tenho uma noção de como será a representação (reta decrescente, crescente; parábola) por causa dos gráficos de Física...
Grata!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dedução da área do círculo.
por Civil UFSCar » Ter Jun 21, 2011 13:24
- 2 Respostas
- 2896 Exibições
- Última mensagem por LuizAquino

Ter Jun 21, 2011 16:08
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de variacao - area do circulo !
por andersoneng » Sex Jun 29, 2012 10:40
- 2 Respostas
- 2918 Exibições
- Última mensagem por Russman

Sex Jun 29, 2012 21:18
Cálculo: Limites, Derivadas e Integrais
-
- A área do círculo determinado pela...
por David_Estudante » Sáb Mai 25, 2013 17:47
- 0 Respostas
- 1105 Exibições
- Última mensagem por David_Estudante

Sáb Mai 25, 2013 17:47
Geometria Analítica
-
- Equação de um Círculo
por Cleyson007 » Qua Abr 07, 2010 11:46
- 4 Respostas
- 1906 Exibições
- Última mensagem por Cleyson007

Qui Abr 08, 2010 12:50
Geometria Analítica
-
- Círculo trigonométrico
 por Ananda » Sex Fev 29, 2008 10:56
por Ananda » Sex Fev 29, 2008 10:56
- 8 Respostas
- 7527 Exibições
- Última mensagem por Ananda

Seg Mar 03, 2008 17:51
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
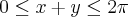 , é igual a:
, é igual a: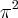 unidades de área
unidades de área
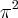 , porque parti de que a área da circunferência é
, porque parti de que a área da circunferência é  .
.

 logo pensamos em desenvolver a soma de arcos.
logo pensamos em desenvolver a soma de arcos. inteiro.
inteiro.

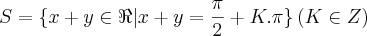
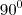

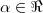 ,
, 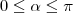 ,
, 
 real,
real, ![\alpha \in [0, \pi] \alpha \in [0, \pi]](/latexrender/pictures/0842c803519eb6c851b3f39181776d01.png) ,
,  ou
ou  , ótimo!
, ótimo!


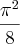

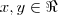 , o primeiro quadrante é a intersecção das regiões representadas por estas inequações:
, o primeiro quadrante é a intersecção das regiões representadas por estas inequações:
 .
.




