 por matematicouff » Dom Mai 20, 2012 04:08
por matematicouff » Dom Mai 20, 2012 04:08
Alguém poderia me ajudar nesse assunto?
Estou com dificuldades em derivação logarítmica. Gostaria de saber como se solucionam essas questões e o que estaria fazendo de errado, já que parto sempre do princípio:
Se
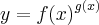
então
![{f}^{\prime}(x)={f(x)}^{g(x)}.\left[{g}^{\prime}(x).lnf(x)+\frac{g(x)}{f(x)}.{f}^{\prime}(x) \right] {f}^{\prime}(x)={f(x)}^{g(x)}.\left[{g}^{\prime}(x).lnf(x)+\frac{g(x)}{f(x)}.{f}^{\prime}(x) \right]](/latexrender/pictures/0bdf6b27eed80b7f18c508e265d3b807.png)
.
Consegui fazer algumas questões dessa maneira, já outras não consegui de forma alguma. Eis algumas:
a)
![f(x)=\frac{{e}^{sen2x.\sqrt[]{x}}}{{e}^{cos3x}} f(x)=\frac{{e}^{sen2x.\sqrt[]{x}}}{{e}^{cos3x}}](/latexrender/pictures/a43de24ad9d8ec72d54d6ea9597cab96.png)
b)
![f(x)={e}^{(\sqrt[]{x})}.ln(\sqrt[]{x}) f(x)={e}^{(\sqrt[]{x})}.ln(\sqrt[]{x})](/latexrender/pictures/a951516a1fbe2b66bca6f925325c721f.png)
c)

d)
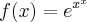
-
matematicouff
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Abr 29, 2012 15:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Ter Mai 22, 2012 14:59
por LuizAquino » Ter Mai 22, 2012 14:59
matematicouff escreveu:Alguém poderia me ajudar nesse assunto?
Estou com dificuldades em derivação logarítmica. Gostaria de saber como se solucionam essas questões e o que estaria fazendo de errado, já que parto sempre do princípio:
Se
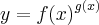
então
![{f}^{\prime}(x)={f(x)}^{g(x)}.\left[{g}^{\prime}(x).lnf(x)+\frac{g(x)}{f(x)}.{f}^{\prime}(x) \right] {f}^{\prime}(x)={f(x)}^{g(x)}.\left[{g}^{\prime}(x).lnf(x)+\frac{g(x)}{f(x)}.{f}^{\prime}(x) \right]](/latexrender/pictures/0bdf6b27eed80b7f18c508e265d3b807.png)
.
Consegui fazer algumas questões dessa maneira, já outras não consegui de forma alguma. Eis algumas:
a)
![f(x)=\frac{{e}^{sen2x.\sqrt[]{x}}}{{e}^{cos3x}} f(x)=\frac{{e}^{sen2x.\sqrt[]{x}}}{{e}^{cos3x}}](/latexrender/pictures/a43de24ad9d8ec72d54d6ea9597cab96.png)
b)
![f(x)={e}^{(\sqrt[]{x})}.ln(\sqrt[]{x}) f(x)={e}^{(\sqrt[]{x})}.ln(\sqrt[]{x})](/latexrender/pictures/a951516a1fbe2b66bca6f925325c721f.png)
c)

d)
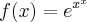
Ao invés de "decorar" a fórmula, o ideal é que você aprenda a técnica.
Eu farei o item a) e você tenta resolver o restante.
Temos que:
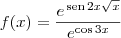
Note que f(x) > 0 para todo x no domínio de f. Desse modo, podemos aplicar o logaritmo natural em ambos os membros e ficar com:
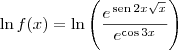
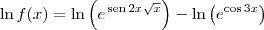
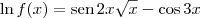
Derivando ambos os membros, temos que:
![\left[\ln f(x)\right]^\prime = \left[\textrm{sen}\,2x\sqrt{x} - \cos 3x\right]^\prime \left[\ln f(x)\right]^\prime = \left[\textrm{sen}\,2x\sqrt{x} - \cos 3x\right]^\prime](/latexrender/pictures/61e0fbdedaaf711fba10993cbf9f85e2.png)
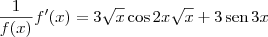
![f^\prime(x) = f(x)\left[3\sqrt{x}\cos 2x\sqrt{x} + 3\,\textrm{sen}\,3x\right] f^\prime(x) = f(x)\left[3\sqrt{x}\cos 2x\sqrt{x} + 3\,\textrm{sen}\,3x\right]](/latexrender/pictures/8abd55d953422fa33424c0d94ed57cf9.png)
![f^\prime(x) = \frac{e^{\,\textrm{sen}\,2x\sqrt{x}}}{e^{\cos 3x}}\left[3\sqrt{x}\cos 2x\sqrt{x} + 3\,\textrm{sen}\,3x\right] f^\prime(x) = \frac{e^{\,\textrm{sen}\,2x\sqrt{x}}}{e^{\cos 3x}}\left[3\sqrt{x}\cos 2x\sqrt{x} + 3\,\textrm{sen}\,3x\right]](/latexrender/pictures/dd794caa12ae173ad359315d1ad5b38c.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivação - derivação logarítmica
por teer4 » Ter Mai 21, 2013 12:11
- 0 Respostas
- 2157 Exibições
- Última mensagem por teer4

Ter Mai 21, 2013 12:11
Cálculo: Limites, Derivadas e Integrais
-
- Derivação
por Michelee » Seg Mai 16, 2011 15:24
- 1 Respostas
- 2223 Exibições
- Última mensagem por LuizAquino

Seg Mai 16, 2011 19:29
Cálculo: Limites, Derivadas e Integrais
-
- [Derivação]
por carolinenonato » Ter Abr 03, 2012 16:30
- 3 Respostas
- 3389 Exibições
- Última mensagem por MarceloFantini

Ter Abr 03, 2012 20:32
Cálculo: Limites, Derivadas e Integrais
-
- Derivação
 por leticiapires52 » Qui Out 22, 2015 11:49
por leticiapires52 » Qui Out 22, 2015 11:49
- 1 Respostas
- 1893 Exibições
- Última mensagem por Cleyson007

Qui Out 22, 2015 20:52
Cálculo: Limites, Derivadas e Integrais
-
- Derivação
 por johnatta » Qui Jun 04, 2015 10:53
por johnatta » Qui Jun 04, 2015 10:53
- 1 Respostas
- 1553 Exibições
- Última mensagem por nakagumahissao

Seg Out 05, 2015 15:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
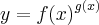 então
então ![{f}^{\prime}(x)={f(x)}^{g(x)}.\left[{g}^{\prime}(x).lnf(x)+\frac{g(x)}{f(x)}.{f}^{\prime}(x) \right] {f}^{\prime}(x)={f(x)}^{g(x)}.\left[{g}^{\prime}(x).lnf(x)+\frac{g(x)}{f(x)}.{f}^{\prime}(x) \right]](/latexrender/pictures/0bdf6b27eed80b7f18c508e265d3b807.png) .
.![f(x)=\frac{{e}^{sen2x.\sqrt[]{x}}}{{e}^{cos3x}} f(x)=\frac{{e}^{sen2x.\sqrt[]{x}}}{{e}^{cos3x}}](/latexrender/pictures/a43de24ad9d8ec72d54d6ea9597cab96.png)
![f(x)={e}^{(\sqrt[]{x})}.ln(\sqrt[]{x}) f(x)={e}^{(\sqrt[]{x})}.ln(\sqrt[]{x})](/latexrender/pictures/a951516a1fbe2b66bca6f925325c721f.png)

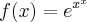


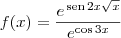
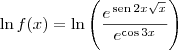
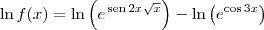
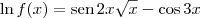
![\left[\ln f(x)\right]^\prime = \left[\textrm{sen}\,2x\sqrt{x} - \cos 3x\right]^\prime \left[\ln f(x)\right]^\prime = \left[\textrm{sen}\,2x\sqrt{x} - \cos 3x\right]^\prime](/latexrender/pictures/61e0fbdedaaf711fba10993cbf9f85e2.png)
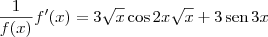
![f^\prime(x) = f(x)\left[3\sqrt{x}\cos 2x\sqrt{x} + 3\,\textrm{sen}\,3x\right] f^\prime(x) = f(x)\left[3\sqrt{x}\cos 2x\sqrt{x} + 3\,\textrm{sen}\,3x\right]](/latexrender/pictures/8abd55d953422fa33424c0d94ed57cf9.png)
![f^\prime(x) = \frac{e^{\,\textrm{sen}\,2x\sqrt{x}}}{e^{\cos 3x}}\left[3\sqrt{x}\cos 2x\sqrt{x} + 3\,\textrm{sen}\,3x\right] f^\prime(x) = \frac{e^{\,\textrm{sen}\,2x\sqrt{x}}}{e^{\cos 3x}}\left[3\sqrt{x}\cos 2x\sqrt{x} + 3\,\textrm{sen}\,3x\right]](/latexrender/pictures/dd794caa12ae173ad359315d1ad5b38c.png)
