jemourafer escreveu:A questão é a seguinte:
-Considere a lemniscata de equação
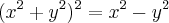
. Determine os quatro pontos de lemniscata em que as retas tangentes são horizontais. Ache, em seguida, os dois pontos em que as tangentes são verticais.
Derivei implicitamente a função sem problemas
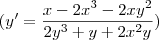
, porém não consigo resolver a equação para achar os pontos onde a reta tangente é horizontal e onde é vertical. Como posso fazer isso?
jemourafer escreveu:Oi

Já estudei sim! Imagino também que pra descobrir os pontos onde a reta tangente é horizontal, basta igualar a zero o numerador. Já os pontos onde a reta tangente é vertical, precisaremos que o denominador valha zero. Meu problema mesmo é em relação à conta pra achar a solução dessas equações.
Para as tangentes horizontais, devemos ter:
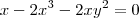

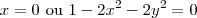
Para o primeiro caso, substituindo x = 0 na equação da lemniscata, ficamos com

. Note que essa equação não tem solução real. Portanto, devemos descartar a possibilidade de x = 0.
Já para o segundo caso, substituindo
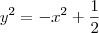
na equação da lemniscata, ficamos com
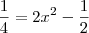
. Note que essa equação tem duas soluções reais. Cada uma dessas soluções irá determinar duas soluções para y. Teremos então os quatro pontos nos quais a reta tangente é horizontal.
Agora basta seguir uma ideia semelhante para determinar os pontos nos quais a reta tangente é vertical. Nesse caso, devemos ter:

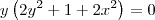

Tente continuar a partir daí.
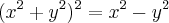 . Determine os quatro pontos de lemniscata em que as retas tangentes são horizontais. Ache, em seguida, os dois pontos em que as tangentes são verticais.
. Determine os quatro pontos de lemniscata em que as retas tangentes são horizontais. Ache, em seguida, os dois pontos em que as tangentes são verticais.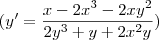 , porém não consigo resolver a equação para achar os pontos onde a reta tangente é horizontal e onde é vertical. Como posso fazer isso?
, porém não consigo resolver a equação para achar os pontos onde a reta tangente é horizontal e onde é vertical. Como posso fazer isso?



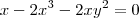

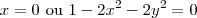
 . Note que essa equação não tem solução real. Portanto, devemos descartar a possibilidade de x = 0.
. Note que essa equação não tem solução real. Portanto, devemos descartar a possibilidade de x = 0.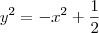 na equação da lemniscata, ficamos com
na equação da lemniscata, ficamos com 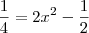 . Note que essa equação tem duas soluções reais. Cada uma dessas soluções irá determinar duas soluções para y. Teremos então os quatro pontos nos quais a reta tangente é horizontal.
. Note que essa equação tem duas soluções reais. Cada uma dessas soluções irá determinar duas soluções para y. Teremos então os quatro pontos nos quais a reta tangente é horizontal.
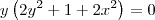




 , avisa que eu resolvo.
, avisa que eu resolvo.

