Sobre esses conjuntos, pode-se afirmar:
a-

B -
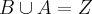
C- A e o conjunto dos numeros pares
Resposta; As 3 estao corretas
ObS;O valor e B n será uma fracao?Sendo assim ele n estaria no conjunto dos racionais?ObrigaDo




danjr5 escreveu:Bmachado,
bom dia!!
A = {..., - 4, - 2, 0, 2, 4, 6,...}
B = {..., - 5, - 3, - 1, 1, 3, 5,...}
A dica nesta questão é que vc 'abra' os conjuntos, fica bem mais fácil visualizá-los.
Espero ter ajudado!!


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: