 por LuizCarlos » Ter Mai 15, 2012 18:57
por LuizCarlos » Ter Mai 15, 2012 18:57
Olá amigo professores, como resolvo uma conta desse tipo!
![\sqrt[]{5+\sqrt[]{24}} \sqrt[]{5+\sqrt[]{24}}](/latexrender/pictures/743f9a80b68560476e80d218e1e6adff.png)
E outra desse tipo:
![\sqrt[]{4.\sqrt[]{6}} \sqrt[]{4.\sqrt[]{6}}](/latexrender/pictures/c8913f0d9893eabbaf3e2da6c1bcf0c9.png)
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Qua Mai 16, 2012 14:30
por LuizCarlos » Qua Mai 16, 2012 14:30
LuizAquino escreveu:LuizCarlos escreveu:Olá amigo professores, como resolvo uma conta desse tipo!
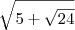
Note que:
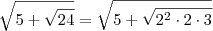
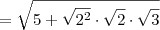
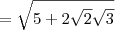
Substituindo 5 por 2 + 3, temos que:
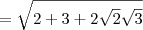
Arrumando essa expressão, temos que:


Lembrando do produto notável
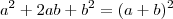
, temos que:
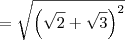
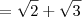
Em resumo, temos que:
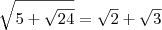
LuizCarlos escreveu:E outra desse tipo:

Note que:
![\sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6} \sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6}](/latexrender/pictures/41fd9b4b73a19ba898a66f853892ecf9.png)
[/quote]
Olá amigo LuizAquino, obrigado por me ajudar! você é muito legal! consegui entender! gostaria de fazer uma pergunta, a única maneira de resolver esses tipos de contas, é da forma como você me ensinou, ou existe outro maneira, pois vejo pessoas resolvendo através de uma fórmula, aquela fórmula de radicais duplos, que por sinal, estava olhando, e não consegui entender direito!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizAquino » Sex Mai 18, 2012 13:26
por LuizAquino » Sex Mai 18, 2012 13:26
LuizCarlos escreveu:(...) a única maneira de resolver esses tipos de contas, é da forma como você me ensinou, ou existe outro maneira, pois vejo pessoas resolvendo através de uma fórmula, aquela fórmula de radicais duplos, que por sinal, estava olhando, e não consegui entender direito!
Eu defendo a ideia de que simplesmente decorar fórmulas prontas não é uma boa estratégia.
Por outro lado, se você sabe deduzir a fórmula, então aí sim você está seguindo uma boa estratégia.
Nesse contexto, eu recomendo que você estude a maneira de deduzir a fórmula para simplificar o chamado radical duplo.
Existem várias páginas na Internet exibindo a dedução. Por exemplo, vide a página abaixo.
Matemática Muito Fácil - Álgebra - Transformação de Radicais Duploshttp://www.matematicamuitofacil.com/radicalduplo.html
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida radiciação
por sullivan » Ter Jan 24, 2012 13:41
- 3 Respostas
- 1898 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 17:00
Álgebra Elementar
-
- Radiciação - Dúvida
por Danilo » Qui Ago 09, 2012 22:37
- 2 Respostas
- 1473 Exibições
- Última mensagem por Danilo

Sex Ago 10, 2012 00:04
Álgebra Elementar
-
- Dúvida - radiciação
por Danilo » Sex Ago 10, 2012 01:53
- 3 Respostas
- 1695 Exibições
- Última mensagem por Danilo

Sex Ago 10, 2012 11:22
Álgebra Elementar
-
- Dúvida - {radiciação}
por Danilo » Sex Ago 10, 2012 11:34
- 2 Respostas
- 1610 Exibições
- Última mensagem por Danilo

Sex Ago 10, 2012 11:47
Álgebra Elementar
-
- Radiciação - dúvida
por Danilo » Sex Ago 10, 2012 18:33
- 2 Respostas
- 1577 Exibições
- Última mensagem por Danilo

Sex Ago 10, 2012 20:01
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{5+\sqrt[]{24}} \sqrt[]{5+\sqrt[]{24}}](/latexrender/pictures/743f9a80b68560476e80d218e1e6adff.png)
![\sqrt[]{4.\sqrt[]{6}} \sqrt[]{4.\sqrt[]{6}}](/latexrender/pictures/c8913f0d9893eabbaf3e2da6c1bcf0c9.png)

![\sqrt[]{5+\sqrt[]{24}} \sqrt[]{5+\sqrt[]{24}}](/latexrender/pictures/743f9a80b68560476e80d218e1e6adff.png)
![\sqrt[]{4.\sqrt[]{6}} \sqrt[]{4.\sqrt[]{6}}](/latexrender/pictures/c8913f0d9893eabbaf3e2da6c1bcf0c9.png)

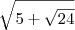 [/quote]
[/quote]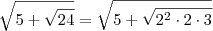
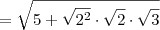
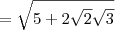
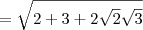


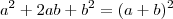 , temos que:
, temos que: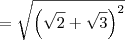
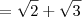
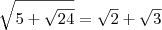
![\sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6} \sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6}](/latexrender/pictures/41fd9b4b73a19ba898a66f853892ecf9.png)

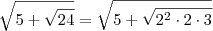
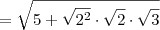
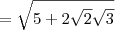
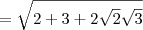


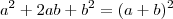 , temos que:
, temos que: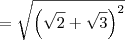
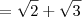
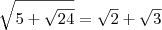
![\sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6} \sqrt{4\cdot \sqrt{6}} = \sqrt{4} \cdot \sqrt{\sqrt{6}} = 2\sqrt[4]{6}](/latexrender/pictures/41fd9b4b73a19ba898a66f853892ecf9.png) [/quote]
[/quote]

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
