[Expressão Númerica] Dúvida ambigua

por **umbrorz** » Qui Mai 10, 2012 15:23

Fala pessoal, minha dúvida é aquela resenha que rolava na internet.

Quanto é o resultado dessa expressão:

6/2(1+2)

É 9 ou 1. :x

VLW !

por **DanielFerreira** » Qui Mai 10, 2012 21:59

$\frac{6}{2(1 + 2)} =$

$\frac{6}{2 + 4} =$

$\frac{6}{6} =$

Agora, se for:
$\frac{6}{2}.(1 + 2) =$

3.(1 + 2) =

Então, Umbrorz
depende do enunciado!
Qual deles vc quis dizer??

por **LuizAquino** » Sex Mai 11, 2012 08:06

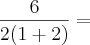
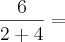
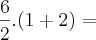
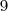
umbrorz escreveu:Fala pessoal, minha dúvida é aquela resenha que rolava na internet.

Quanto é o resultado dessa expressão:

6/2(1+2)

É 9 ou 1. :x

danjr5 escreveu: $\frac{6}{2(1 + 2)} =$

$\frac{6}{2 + 4} =$

$\frac{6}{6} =$

Agora, se for:
$\frac{6}{2}.(1 + 2) =$

Então, Umbrorz
depende do enunciado!
Qual deles vc quis dizer??

A notação dada por "6/2(1+2)" é equivalente a notação $\frac{6}{2}(1 + 2)$ .

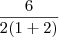Se o objetivo fosse a notação $\frac{6}{2(1 + 2)}$ , então a forma correta equivalente seria 6/[2(1 + 2)].

Note a importância do uso adequado dos delimitadores (isto é, "( )", "[ ]" e "{ }").

Sendo assim, o correto é afirmar que 6/2(1+2) = 9.

Por outro lado, temos que 6/[2(1+2)] = 1.