 por iceman » Qui Mai 10, 2012 18:52
por iceman » Qui Mai 10, 2012 18:52
Olá galera, sou novo aqui no fórum e ficaria muito agradecido se pudessem me ajudar em algumas questões, aí vai a segunda questão:
Ache "m" para que o número complexo
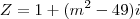
seja um número real.
a) 1
b) 3 e -3
c) 9 e -9
d) 7 e -7
e)NDA
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qui Mai 10, 2012 19:25
por fraol » Qui Mai 10, 2012 19:25
Boa noite,
Para que o número complexo
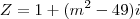
seja um número real, ele não deve ter a parte imaginária.
Então o coeficiente de

deve ser igual a 0.
Qual é o coeficiente de

no número complexo dado?
Iguale esse coeficiente a 0 e resolva a equação para obter a resposta.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por iceman » Qui Mai 10, 2012 19:33
por iceman » Qui Mai 10, 2012 19:33
fraol escreveu:Boa noite,
Para que o número complexo
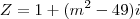
seja um número real, ele não deve ter a parte imaginária.
Então o coeficiente de

deve ser igual a 0.
Qual é o coeficiente de

no número complexo dado?
Iguale esse coeficiente a 0 e resolva a equação para obter a resposta.
.
Amigo, o problema é que eu não sei como que é que faz D; Você poderia montar o cálculo para mim ? Obrigado pela atenção!
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qui Mai 10, 2012 19:40
por fraol » Qui Mai 10, 2012 19:40
- Código: Selecionar todos
Qual é o coeficiente de no número complexo dado?

Iguale esse coeficiente a 0 e resolva a equação para obter a resposta.

Veja que agora você tem uma equação do 2o. grau. Tente resolvê-la.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por iceman » Qui Mai 10, 2012 19:47
por iceman » Qui Mai 10, 2012 19:47
fraol escreveu:- Código: Selecionar todos
Qual é o coeficiente de no número complexo dado?
A questão é assim mesmo, coloquei ela certinha aqui, o

é daquele jeito.
-
iceman
- Usuário Parceiro

-
- Mensagens: 70
- Registrado em: Qui Mai 10, 2012 18:35
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qui Mai 10, 2012 21:15
por fraol » Qui Mai 10, 2012 21:15
Caro
iceman,
Eu entendi a questão e estava lhe perguntando, de uma maneira a indicar o caminho para a solução.
Para resolver questões como essa você deve saber, como pré-requisito, quais são as partes real e imaginária e qual é a relação que as mesmas devem satisfazer para se saber quando o complexo é real puro ou imaginário puro.
De qualquer forma respondi as questões que lhe fiz e agora basta que você resolva a equação do segundo grau para chegar ao resultado.
Bom estudo.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números Complexos - Dúvida
por iceman » Ter Mai 15, 2012 20:22
- 1 Respostas
- 1809 Exibições
- Última mensagem por fraol

Ter Mai 15, 2012 22:20
Números Complexos
-
- Dúvida - Números complexos
por Danilo » Sex Ago 03, 2012 02:05
- 5 Respostas
- 3843 Exibições
- Última mensagem por Danilo

Sex Ago 03, 2012 16:46
Números Complexos
-
- Dúvida - números complexos
por Danilo » Ter Ago 07, 2012 14:51
- 4 Respostas
- 3125 Exibições
- Última mensagem por LuizAquino

Qua Ago 08, 2012 11:38
Números Complexos
-
- Números complexos {dúvida}
por Danilo » Dom Ago 26, 2012 19:59
- 4 Respostas
- 3613 Exibições
- Última mensagem por MarceloFantini

Sex Set 21, 2012 23:53
Números Complexos
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17106 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
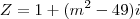 seja um número real.
seja um número real.
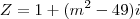 seja um número real.
seja um número real.
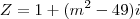 seja um número real, ele não deve ter a parte imaginária.
seja um número real, ele não deve ter a parte imaginária. deve ser igual a 0.
deve ser igual a 0.  no número complexo dado?
no número complexo dado? 
seja um número real, ele não deve ter a parte imaginária.
deve ser igual a 0.
no número complexo dado?












