 por Pri Ferreira » Qui Mai 10, 2012 15:55
por Pri Ferreira » Qui Mai 10, 2012 15:55
Feita uma pesquisa em determinada escola sobre a preferência dos alunos por esporte obteve-se o seguinte
resultado.
� 60% dos alunos gostam de dança.
� 55% dos alunos gostam de ginástica.
� 10% dos alunos não gostam nem de dança nem de ginástica.
� 50 pessoas gostam tanto de dança quanto de ginástica.
Com os dados acima podemos afirmar que foram entrevistados um total de:
A) 100 alunos D) 200 alunos
B) 150 alunos E) 300 alunos
C) 500 alunos
Gostaria de ver a resolução dessa questão!!
Por favor!!!
-
Pri Ferreira
- Usuário Parceiro

-
- Mensagens: 59
- Registrado em: Qua Out 19, 2011 20:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: formado
 por fraol » Qui Mai 10, 2012 19:35
por fraol » Qui Mai 10, 2012 19:35
Boa noite,
Seja A o número de Alunos entrevistados.
Então A será igual à:
Total de alunos que gostam de Dança = 60%A
Mais o total de alunos que gostam de Ginástica = 55%A
Menos o total de alunos que gostam de Dança e Ginástica = 50 alunos
Mais o total de alunos que gostam nem de dança nem de ginástica = 10%A.
Ou seja: A = 60%A + 55%A - 50 + 10%A.
Veja se consegue concluir a partir daí.
Qualquer dúvida retorne.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por LuizCarlos » Qui Mai 10, 2012 21:14
por LuizCarlos » Qui Mai 10, 2012 21:14
fraol escreveu:Boa noite,
Seja A o número de Alunos entrevistados.
Então A será igual à:
Total de alunos que gostam de Dança = 60%A
Mais o total de alunos que gostam de Ginástica = 55%A
Menos o total de alunos que gostam de Dança e Ginástica = 50 alunos
Mais o total de alunos que gostam nem de dança nem de ginástica = 10%A.
Ou seja: A = 60%A + 55%A - 50 + 10%A.
Veja se consegue concluir a partir daí.
Qualquer dúvida retorne.
.
Olá amigo fraol, resolvi essa questão, encontrei o resultado
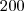
, mas gostaria de saber, porque temos que descontar o número de alunos que gostam tanto de dança como de ginástica!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por fraol » Qui Mai 10, 2012 21:44
por fraol » Qui Mai 10, 2012 21:44
Caro
LuizCarlos,
Vamos analisar alguns casos envolvendo dois conjuntos A e B:
a) Eles podem não ter elementos em comum. Nesse caso o número total de elementos é igual a soma dos números de elementos de cada conjunto. Por exemplo A com 5 elementos e B com 3 elementos. Assim o total de elementos é igua a 5 + 3 = 8.
b) Eles podem podem ter um ou mais elementos em comum. Nesse caso devemos descontar o número de elementos em comum, caso contrário estaríamos contando duas vezes cada um desses elementos comuns. Por exemplo A com 5 elementos e B com 3 elementos, sendo que 1 elemento é comum a ambos. Assim o total de elementos é igual a 5 + 3
- 1 = 7.
Caso não esteja claro retorne.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por DanielFerreira » Qui Mai 10, 2012 22:08
por DanielFerreira » Qui Mai 10, 2012 22:08
O que foi dito pelo Fraol, pode ser visualizado no Diagrama de Venn.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizCarlos » Qui Mai 10, 2012 23:16
por LuizCarlos » Qui Mai 10, 2012 23:16
fraol escreveu:Caro
LuizCarlos,
Vamos analisar alguns casos envolvendo dois conjuntos A e B:
a) Eles podem não ter elementos em comum. Nesse caso o número total de elementos é igual a soma dos números de elementos de cada conjunto. Por exemplo A com 5 elementos e B com 3 elementos. Assim o total de elementos é igua a 5 + 3 = 8.
b) Eles podem podem ter um ou mais elementos em comum. Nesse caso devemos descontar o número de elementos em comum, caso contrário estaríamos contando duas vezes cada um desses elementos comuns. Por exemplo A com 5 elementos e B com 3 elementos, sendo que 1 elemento é comum a ambos. Assim o total de elementos é igual a 5 + 3
- 1 = 7.
Caso não esteja claro retorne.
.
Olá amigo, fraol, muito obrigado por me ajudar na minha dúvida! consegui entender o que você explicou, mas não consegui levar essa explicação, associar ela com aquela questão proposta! ainda não caiu a ficha!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Qui Mai 10, 2012 23:17
por LuizCarlos » Qui Mai 10, 2012 23:17
danjr5 escreveu:O que foi dito pelo Fraol, pode ser visualizado no Diagrama de Venn.
Olá amigo danjr5, ainda não estudei esse Diagrama de Venn, vou pesquisar a respeito!

-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por fraol » Qui Mai 10, 2012 23:31
por fraol » Qui Mai 10, 2012 23:31
LuizCarlos escreveu:
Olá amigo, fraol, muito obrigado por me ajudar na minha dúvida! consegui entender o que você explicou, mas não consegui levar essa explicação, associar ela com aquela questão proposta! ainda não caiu a ficha!
Eu apliquei esse raciocínio em
Ou seja: A = 60%A + 55%A - 50 + 10%A
Veja que 50 é o número de alunos que gostam de dança e ginástica. Então descontamos o 50 em
60%A + 55%A - 50
para não contar duas vezes os alunos que gostam de ambas as modalidades.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por LuizCarlos » Sex Mai 11, 2012 01:16
por LuizCarlos » Sex Mai 11, 2012 01:16
fraol escreveu:LuizCarlos escreveu:
Olá amigo, fraol, muito obrigado por me ajudar na minha dúvida! consegui entender o que você explicou, mas não consegui levar essa explicação, associar ela com aquela questão proposta! ainda não caiu a ficha!
Eu apliquei esse raciocínio em
Ou seja: A = 60%A + 55%A - 50 + 10%A
Veja que 50 é o número de alunos que gostam de dança e ginástica. Então descontamos o 50 em
60%A + 55%A - 50
para não contar duas vezes os alunos que gostam de ambas as modalidades.
.
Consegui entender fraol, legal, essa questão até que não é difícil, basta entender, o raciocínio empregado que resolvemos tranquilame! muito obrigado pela ajuda! abraço.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de concurso...
por henrivoador » Seg Abr 19, 2010 20:37
- 7 Respostas
- 11294 Exibições
- Última mensagem por henrivoador

Seg Abr 26, 2010 13:07
Logaritmos
-
- Questão de concurso
por bia rosendo » Qua Fev 23, 2011 11:00
- 4 Respostas
- 5804 Exibições
- Última mensagem por Elcioschin

Qui Fev 24, 2011 11:08
Funções
-
- Questão de concurso
 por bia rosendo » Seg Fev 28, 2011 22:54
por bia rosendo » Seg Fev 28, 2011 22:54
- 2 Respostas
- 7741 Exibições
- Última mensagem por LuizAquino

Ter Mar 01, 2011 14:12
Problemas do Cotidiano
-
- QUESTAO CONCURSO..
por PathyNorato » Qui Jul 07, 2011 15:59
- 1 Respostas
- 3511 Exibições
- Última mensagem por FilipeCaceres

Qui Jul 07, 2011 21:05
Matemática Financeira
-
- questão de concurso
por luciana-lopfer » Qui Nov 24, 2011 14:34
- 5 Respostas
- 6369 Exibições
- Última mensagem por Tiago_Cariolano

Seg Jan 16, 2012 01:23
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



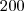 , mas gostaria de saber, porque temos que descontar o número de alunos que gostam tanto de dança como de ginástica!
, mas gostaria de saber, porque temos que descontar o número de alunos que gostam tanto de dança como de ginástica!


 .
.



