 por MERLAYNE » Qua Mai 09, 2012 11:08
por MERLAYNE » Qua Mai 09, 2012 11:08
O conjunto solução da inequação

é :
-
MERLAYNE
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Mar 28, 2012 19:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Qua Mai 09, 2012 12:29
por Cleyson007 » Qua Mai 09, 2012 12:29
Bom dia Merlayne!
Vou te dar a dica e você tenta resolver, ok?
Multiplique cruzado. Veja:
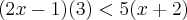
Comente qualquer dúvida

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por DanielFerreira » Qua Mai 09, 2012 22:48
por DanielFerreira » Qua Mai 09, 2012 22:48
Cleyson,
em inequação não devemos multiplicar cruzado!!
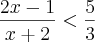




Merlayne,
caímos numa inequação quociente, sabe como prosseguir agora??
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Inequação quociente
 por Bruno Pinheiro » Ter Dez 28, 2010 01:12
por Bruno Pinheiro » Ter Dez 28, 2010 01:12
- 3 Respostas
- 3029 Exibições
- Última mensagem por MarceloFantini

Qua Dez 29, 2010 10:45
Álgebra Elementar
-
- Inequação Quociente
por Luis_Hgl » Qua Fev 27, 2013 13:18
- 1 Respostas
- 3121 Exibições
- Última mensagem por young_jedi

Sex Mar 01, 2013 23:13
Inequações
-
- Inequação-quociente
 por Celma » Dom Jul 21, 2013 11:42
por Celma » Dom Jul 21, 2013 11:42
- 6 Respostas
- 3873 Exibições
- Última mensagem por Celma

Seg Jul 22, 2013 19:15
Inequações
-
- inequação produto/quociente
por vhcs29 » Qui Abr 01, 2010 12:32
- 2 Respostas
- 5299 Exibições
- Última mensagem por vhcs29

Sex Abr 02, 2010 12:59
Álgebra Elementar
-
- Inequação Quociente (Módulo)
por Rafael16 » Sex Jul 06, 2012 12:43
- 1 Respostas
- 2193 Exibições
- Última mensagem por Russman

Sex Jul 06, 2012 17:24
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é :
é :

 é :
é :
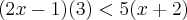


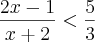






 .
.



