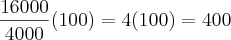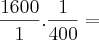Boa tarde Babara!
Fico feliz em poder ajudar..
Estou pensando de uma outra forma e acredito que o gabarito está correto. Veja só:
Estamos trabalhando com porcentagens, vamos supor que seja para algum valor em reais --> Exemplo: R$ 1.000,00
1600% de R$ 1.000,00 = (1600%)(1.000,00) / 100% (Regra de três simples - Repare que o sinal de porcentagem "some" e teremos um valor em R$).
1600% de R$ 1.000,00 = R$ 16.000,00
Façamos o mesmo para 400%. Acompanhe:
400% de R$ 1.000,00 = (400%)(1.000,00) / 100% (Regra de três simples - O sinal de porcentagem "some", restando o valor em R$).
400% de R$ 1.000,00 = R$ 4.000,00
Jogando no problema, temos:
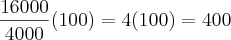
Barbara, vamos ver se alguém comenta algo. Mas, acredito realmente seja isso e não cabe recurso.
Comente qualquer dúvida

Atenciosamente,
Cleyson007