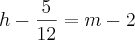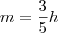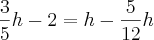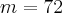por Raphael Feitas10 » Seg Mai 07, 2012 14:45
por Raphael Feitas10 » Seg Mai 07, 2012 14:45
Em um local existem homens e mulheres. A quantidade de melheres era 3/5 dos homens, se 5/12 dos homens e duas mulheres saissem ficariam quantidades iguais.Quantos homens e mulheres existiam. R: 120 e 72
Brother eu montei essa questão desse jeito aqui...

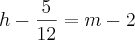
Fiz uma parecida desse memos jeito e bateu as respostas mais essa aqui ñ obtive hêsito será q essa questão ta mal formulada ou eu q montei errado me ajuda aew parceiro desde de já muito agradecido...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Raphael Feitas10 » Ter Mai 08, 2012 00:49
por Raphael Feitas10 » Ter Mai 08, 2012 00:49
Me ajuda aew galera por favor...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FelipeMS » Ter Mai 08, 2012 01:42
por FelipeMS » Ter Mai 08, 2012 01:42
(i)
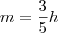
Para que a quantidade de homens seja igual a de mulheres:
(ii)

Substituindo (i) em (ii):
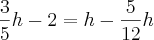
Acha-se então h:

Substituindo o valor de h em (i), acha-se o número de mulheres:
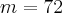
Assim:

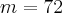
-
FelipeMS
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 08, 2012 01:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números inteiros
por thadeu » Qui Nov 19, 2009 11:41
- 2 Respostas
- 2066 Exibições
- Última mensagem por thadeu

Qui Nov 19, 2009 13:46
Álgebra Elementar
-
- numeros inteiros
por edwilsoncrep » Qui Mar 04, 2010 20:03
- 5 Respostas
- 6387 Exibições
- Última mensagem por adriana_borges

Dom Mai 09, 2010 12:04
Sequências
-
- Numeros inteiros
por Raphael Feitas10 » Qua Jan 05, 2011 00:16
- 3 Respostas
- 2680 Exibições
- Última mensagem por PedroSantos

Qua Jan 05, 2011 19:49
Cálculo: Limites, Derivadas e Integrais
-
- Numeros inteiros
por Raphael Feitas10 » Qui Jan 13, 2011 13:18
- 15 Respostas
- 9678 Exibições
- Última mensagem por Raphael Feitas10

Qua Jan 19, 2011 00:40
Números Complexos
-
- Numeros inteiros 2
por Raphael Feitas10 » Qua Jan 19, 2011 00:28
- 1 Respostas
- 2891 Exibições
- Última mensagem por Renato_RJ

Qua Jan 19, 2011 01:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.