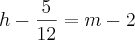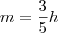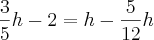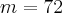por Raphael Feitas10 » Seg Mai 07, 2012 14:45
por Raphael Feitas10 » Seg Mai 07, 2012 14:45
Em um local existem homens e mulheres. A quantidade de melheres era 3/5 dos homens, se 5/12 dos homens e duas mulheres saissem ficariam quantidades iguais.Quantos homens e mulheres existiam. R: 120 e 72
Brother eu montei essa questão desse jeito aqui...

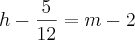
Fiz uma parecida desse memos jeito e bateu as respostas mais essa aqui ñ obtive hêsito será q essa questão ta mal formulada ou eu q montei errado me ajuda aew parceiro desde de já muito agradecido...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Raphael Feitas10 » Ter Mai 08, 2012 00:49
por Raphael Feitas10 » Ter Mai 08, 2012 00:49
Me ajuda aew galera por favor...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por FelipeMS » Ter Mai 08, 2012 01:42
por FelipeMS » Ter Mai 08, 2012 01:42
(i)
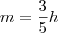
Para que a quantidade de homens seja igual a de mulheres:
(ii)

Substituindo (i) em (ii):
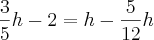
Acha-se então h:

Substituindo o valor de h em (i), acha-se o número de mulheres:
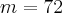
Assim:

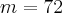
-
FelipeMS
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mai 08, 2012 01:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números inteiros
por thadeu » Qui Nov 19, 2009 11:41
- 2 Respostas
- 2064 Exibições
- Última mensagem por thadeu

Qui Nov 19, 2009 13:46
Álgebra Elementar
-
- numeros inteiros
por edwilsoncrep » Qui Mar 04, 2010 20:03
- 5 Respostas
- 6382 Exibições
- Última mensagem por adriana_borges

Dom Mai 09, 2010 12:04
Sequências
-
- Numeros inteiros
por Raphael Feitas10 » Qua Jan 05, 2011 00:16
- 3 Respostas
- 2678 Exibições
- Última mensagem por PedroSantos

Qua Jan 05, 2011 19:49
Cálculo: Limites, Derivadas e Integrais
-
- Numeros inteiros
por Raphael Feitas10 » Qui Jan 13, 2011 13:18
- 15 Respostas
- 9674 Exibições
- Última mensagem por Raphael Feitas10

Qua Jan 19, 2011 00:40
Números Complexos
-
- Numeros inteiros 2
por Raphael Feitas10 » Qua Jan 19, 2011 00:28
- 1 Respostas
- 2889 Exibições
- Última mensagem por Renato_RJ

Qua Jan 19, 2011 01:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.