Numa sala de aula existem 3 filas de mesas, cada fila com 10 cadeiras.Ao distribuir 30 alunos pelos 30 lugares,qual a probabilidade de um grupo de 3 amigos ficarem na mesma fila?
Os casos possíveis serão iguais a 30!
A minha dúvida está nos casos favoráveis.
O gabarito é
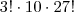
A meu ver, por cada arranjo que os 3 amigos ocuparem em cada fila, os restantes alunos podem permutar 27! formas diferentes nas restantes 27 cadeiras. Ora os 3 amigos podem sentar-se em cada fila de A(10,3)=720 maneiras diferentes. Não consigo entender o gabarito!
Alguém me pode ajudar?
Obrigado


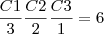

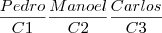
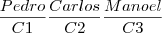
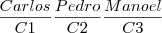
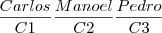
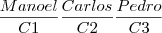
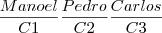
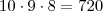 . Ou seja é uma premutação
. Ou seja é uma premutação 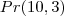 .
.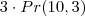 . Mas como a ordem conta, a posição de cada um dos restantes 27 alunos é importante. Por isso por cada posição que os 3 amigos ocupem nas diferentes filas, os restantes alunos podem permutar
. Mas como a ordem conta, a posição de cada um dos restantes 27 alunos é importante. Por isso por cada posição que os 3 amigos ocupem nas diferentes filas, os restantes alunos podem permutar 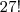 .
.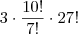 . Só posso concluir que o gabarito está errado!!!!!!!
. Só posso concluir que o gabarito está errado!!!!!!!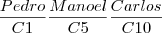
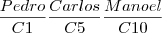
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.