por dekol2 » Dom Mai 06, 2012 20:39
Olá! estou com uma certa dificuldade para derivar uma função, se alguém poder me ajudar agradeço
f(x)=
-
dekol2
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Dom Mai 06, 2012 20:26
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
por Claudin » Dom Mai 06, 2012 21:41
Basta seguir as regras de derivação
assim temos que:
![\frac{f(x)}{g(x)}= \frac{f\prime(x)g(x)-f(x)g\prime(x)}{[g(x)]^2}](/latexrender/pictures/4828967540dd3589abad0746a7105771.png "\frac{f(x)}{g(x)}= \frac{f\prime(x)g(x)-f(x)g\prime(x)}{[g(x)]^2}")
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário
-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
por dekol2 » Seg Mai 07, 2012 01:07
Conheço a regra do quociente, mas se fosse possível gostaria de ver o desenvolvimento do problema para tirar uma duvida, pois em uma vídeo aula o professor pôs o resultado da derivada direta e não desenvolveu, e estou tendo dificuldades para desenvolve-la.
-
dekol2
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Dom Mai 06, 2012 20:26
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
por DanielFerreira » Seg Mai 07, 2012 02:21
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação
-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
por LuizAquino » Seg Mai 07, 2012 11:34
dekol2 escreveu:Olá! estou com uma certa dificuldade para derivar uma função, se alguém poder me ajudar agradeço
f(x)=
- figura.png (4.96 KiB) Exibido 3121 vezes
Por favor, procure usar o LaTeX para inserir em sua mensagem as notações desejadas. Vide o tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74Inclusive, o uso do LaTeX para escrever as notações faz parte das
Regras deste Fórum (regra 2).
dekol2 escreveu:Conheço a regra do quociente, mas se fosse possível gostaria de ver o desenvolvimento do problema para tirar uma duvida, pois em uma vídeo aula o professor pôs o resultado da derivada direta e não desenvolveu, e estou tendo dificuldades para desenvolve-la.
Apenas para referência, a derivada dessa função aparece na videoaula "21. Cálculo I - Teste da Primeira e da Segunda Derivada". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-
LuizAquino
- Colaborador Moderador - Professor
-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 10492 Exibições
- Última mensagem por Cleyson007
Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Quociente
por Paraujo » Dom Set 23, 2012 21:15
- 9 Respostas
- 4870 Exibições
- Última mensagem por Paraujo
Ter Set 25, 2012 12:15
Cálculo: Limites, Derivadas e Integrais
-
- Derivada quociente.
por Sobreira » Seg Out 29, 2012 16:24
- 3 Respostas
- 2270 Exibições
- Última mensagem por young_jedi
Seg Out 29, 2012 17:58
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida com derivada do quociente
por arnoanderson » Seg Nov 02, 2009 12:08
- 2 Respostas
- 3479 Exibições
- Última mensagem por arnoanderson
Ter Nov 03, 2009 09:36
Cálculo: Limites, Derivadas e Integrais
-
- Exercício Derivada do Quociente
por Tayron » Qua Fev 09, 2011 16:35
- 1 Respostas
- 5059 Exibições
- Última mensagem por LuizAquino
Qua Fev 09, 2011 17:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja
o ângulo entre o eixo horizontal e o afixo
. O triângulo é retângulo com catetos
e
, tal que
. Seja
o ângulo complementar. Então
. Como
, o ângulo que o afixo
formará com a horizontal será
, mas negativo pois tem de ser no quarto quadrante. Se
, então
. Como módulo é um:
.
Logo, o afixo é
.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
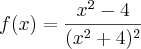
![f'(x) = \frac{2x.(x^2 + 4)^2 - (x^2 - 4).2.(x^2 + 4)^1.2x}{[(x^2 + 4)^2]^2}](/latexrender/pictures/49cf111a77a5d336b578ae514a037a94.png "f'(x) = \frac{2x.(x^2 + 4)^2 - (x^2 - 4).2.(x^2 + 4)^1.2x}{[(x^2 + 4)^2]^2}")
![f'(x) = \frac{2x(x^2 + 4)[(x^2 + 4) - 2(x^2 - 4)]}{(x^2 + 4)^4}](/latexrender/pictures/25e215fa938e1485e70996d980a6252a.png "f'(x) = \frac{2x(x^2 + 4)[(x^2 + 4) - 2(x^2 - 4)]}{(x^2 + 4)^4}")
![f'(x) = \frac{2x[(x^2 + 4) - 2(x^2 - 4)]}{(x^2 + 4)^3}](/latexrender/pictures/c7bf169d5e34298c0c504c3e90f0be99.png "f'(x) = \frac{2x[(x^2 + 4) - 2(x^2 - 4)]}{(x^2 + 4)^3}")
![f'(x) = \frac{2x[x^2 + 4 - 2x^2 + 8]}{(x^2 + 4)^3}](/latexrender/pictures/343cc58dfdf3458156e709d7e08c07d2.png "f'(x) = \frac{2x[x^2 + 4 - 2x^2 + 8]}{(x^2 + 4)^3}")
![f'(x) = \frac{2x[- x^2 + 12]}{(x^2 + 4)^3}](/latexrender/pictures/9f7edd2c0cbae91c16f00bc0106ecf74.png "f'(x) = \frac{2x[- x^2 + 12]}{(x^2 + 4)^3}")
