 por Fabio Wanderley » Dom Abr 29, 2012 16:53
por Fabio Wanderley » Dom Abr 29, 2012 16:53
Olá pessoal. Fiquei em dúvida a respeito do gabarito dessa questão:
Em um conjunto E de empresas, indica-se por

o subconjunto de E formado pelas empresas que já participaram de pelo menos
x procedimentos licitatórios, em que
x = 0, 1, 2, ..., e por

a quantidade de elementos do conjunto

. Julgue os itens seguintes a respeito desses conjuntos.
( ) Se x e y forem números inteiros não negativos e x  y, então
y, então 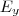

 .
.Gabarito:
CEu marquei
E, pois como y é maior que x, concluí que o subconjunto Ex está contido no Ey, e não o contrário. Alguém pode me explicar o gabarito.
Desde já agradeço!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por MarceloFantini » Sáb Mai 05, 2012 20:54
por MarceloFantini » Sáb Mai 05, 2012 20:54
Fábio, você não colocou as opções para avaliarmos e entendermos o seu raciocínio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fabio Wanderley » Seg Mai 28, 2012 22:15
por Fabio Wanderley » Seg Mai 28, 2012 22:15
MarceloFantini escreveu:Fábio, você não colocou as opções para avaliarmos e entendermos o seu raciocínio.
Marcelo, é uma questão para julgar certo (C) ou errado (E)... daí eu julguei errado, baseando no que expliquei.
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por MarceloFantini » Seg Mai 28, 2012 22:49
por MarceloFantini » Seg Mai 28, 2012 22:49
Tome

e

. Então

e
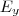
representa empresas que participaram de
pelo menos dois procedimentos, enquanto que

representa empresas que participaram de
pelo menos um procedimento. Quem participou de pelo menos dois
com certeza participou de pelo menos um, logo
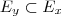
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [PA] Uma dúvida numa questão de PA
por rochadapesada » Qui Abr 04, 2013 22:08
- 3 Respostas
- 2633 Exibições
- Última mensagem por DanielFerreira

Dom Abr 07, 2013 20:28
Progressões
-
- [teoria de limites] dúvida numa questão de prova
por Fabio Wanderley » Sex Abr 13, 2012 23:38
- 2 Respostas
- 1943 Exibições
- Última mensagem por Fabio Wanderley

Sáb Abr 14, 2012 00:43
Cálculo: Limites, Derivadas e Integrais
-
- Questão de Conjunto - dúvida
por marinalcd » Qui Jul 30, 2015 16:07
- 1 Respostas
- 1984 Exibições
- Última mensagem por nakagumahissao

Sex Jul 31, 2015 12:14
Conjuntos
-
- Questão CESPE 2013
 por Isis » Sex Abr 25, 2014 19:54
por Isis » Sex Abr 25, 2014 19:54
- 9 Respostas
- 8442 Exibições
- Última mensagem por vitorms

Qua Dez 03, 2014 14:52
Lógica
-
- me ajudem! questão cespe raciocínio
por leandro moraes » Qui Jun 10, 2010 08:49
- 0 Respostas
- 1212 Exibições
- Última mensagem por leandro moraes

Qui Jun 10, 2010 08:49
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 o subconjunto de E formado pelas empresas que já participaram de pelo menos x procedimentos licitatórios, em que x = 0, 1, 2, ..., e por
o subconjunto de E formado pelas empresas que já participaram de pelo menos x procedimentos licitatórios, em que x = 0, 1, 2, ..., e por  a quantidade de elementos do conjunto
a quantidade de elementos do conjunto  . Julgue os itens seguintes a respeito desses conjuntos.
. Julgue os itens seguintes a respeito desses conjuntos. y, então
y, então 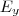

 .
.



 e
e  . Então
. Então  e
e 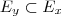 .
.