 e
e  e tem centro na reta
e tem centro na reta 

 e
e  e tem centro na reta
e tem centro na reta 

Claudin escreveu:Determine a equação da circunferência que contém os pontose
e tem centro na reta
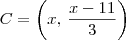 .
.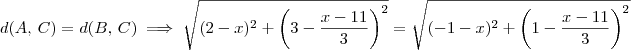

![\sqrt[]{\frac{10x^2-156x+436}{9}}= \sqrt[]{\frac{10x^2-66x+205}{9}} \sqrt[]{\frac{10x^2-156x+436}{9}}= \sqrt[]{\frac{10x^2-66x+205}{9}}](/latexrender/pictures/28e4f17db53b14530a644c4727938845.png)

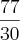

Claudin escreveu:Encontrei um resultado incoerente
Poderia me ajudar?
Cheguei até
Extrai a raiz, e acabei achando um valor negativo para x.
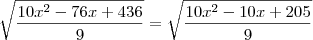

![\sqrt[]{(Xc - Xa)^2 + (Yc - Ya)^2} \sqrt[]{(Xc - Xa)^2 + (Yc - Ya)^2}](/latexrender/pictures/199cef608dbeffbf196f181db887bded.png)
![\sqrt[]{(x-2)^2 + (\frac{x-11}{3}-1)^2}= \sqrt[]{(x+1)^2+(\frac{x-11}{3}-1)^2} \sqrt[]{(x-2)^2 + (\frac{x-11}{3}-1)^2}= \sqrt[]{(x+1)^2+(\frac{x-11}{3}-1)^2}](/latexrender/pictures/d1291eb60e2c7bed60100c51ced2d393.png)
![\sqrt[]{(x^2-4x+4)+(\frac{x-20}{3})^2} = \sqrt[]{(x^2+2x+1)+(\frac{x-14}{3})^2} \sqrt[]{(x^2-4x+4)+(\frac{x-20}{3})^2} = \sqrt[]{(x^2+2x+1)+(\frac{x-14}{3})^2}](/latexrender/pictures/7a50c3a6bc83bc981ccf1472c5deaa8a.png)

Claudin escreveu:
até aqui tudo certo?
Já refiz várias vezes e não encontro resultado.

![\sqrt[]{(x^2-4x+4)+(\frac{x^2}{3}-\frac{40x}{3}+\frac{400}{9})}= \sqrt[]{(x^2+2x+1)+(\frac{x^2}{9}-\frac{28x}{3}+\frac{196}{9})} \sqrt[]{(x^2-4x+4)+(\frac{x^2}{3}-\frac{40x}{3}+\frac{400}{9})}= \sqrt[]{(x^2+2x+1)+(\frac{x^2}{9}-\frac{28x}{3}+\frac{196}{9})}](/latexrender/pictures/9ababdc4128405948fd0a23cb7ce1a46.png)

Claudin escreveu:
Acho então que meu erro deve esta a partir desse ponto
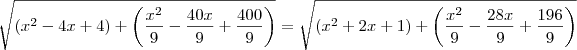

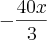 e
e 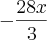 ?
?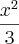 foi erro de digitação mesmo.
foi erro de digitação mesmo.
Claudin escreveu:Eu achava que ficariae
?
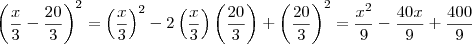

LuizAquino escreveu:Refaça suas contas, pois você deveria encontrar:
Agora tente continuar a partir daí.
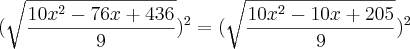

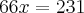
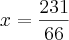
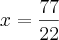
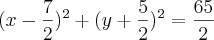

Claudin escreveu:Consegui chegar até aqui.
Logo depois elevei ambos os membros ao quadrado
O que achei meio estranho, pois no caso encontrei o raio
Sendo que a resposta seria
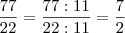



Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)