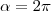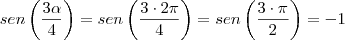Ao olharmos esta equação:
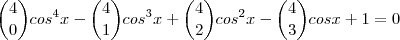
Os coeficientes lembram o triângulo de Pascal, veja:
Pois também pode ser escrita assim:
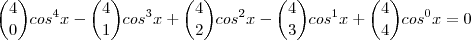
-Ou ainda, podemos lembrar dele após o desenvolvimento que você fez dos números binomiais, vendo os coeficientes na quinta linha:
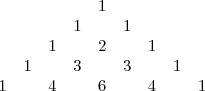
Um assunto relacionado é o desenvolvimento da potência n-ésima do binômio

, veja:
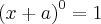

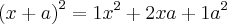
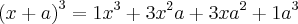
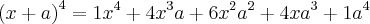
Note que os coeficientes de cada desenvolvimento formam a linha do triângulo de Pascal, sendo o número da linha igual ao expoente de

.
É a chamada
identidade do binômio de Newton:
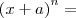
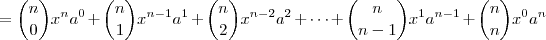
Então, podemos identificar esta identidade na equação dada para simplificá-la.
Para isso, ela ainda pode ser convenientemente reescrita assim:
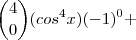
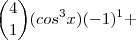
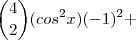
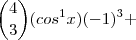
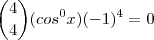
Portanto, agora a potência do binômio de Newton (antes do desenvolvimento) fica mais evidente, simplificando nossa equação, veja:
![\left[ cosx + (-1) \right] ^4 = 0 \left[ cosx + (-1) \right] ^4 = 0](/latexrender/pictures/6c53264e2db19b48a86fb1ed4dfb30c4.png)
Vamos então resolvê-la:
![\left[ cosx + (-1) \right] ^2 \cdot \left[ cosx + (-1) \right] ^2 = 0 \left[ cosx + (-1) \right] ^2 \cdot \left[ cosx + (-1) \right] ^2 = 0](/latexrender/pictures/ee5e1ff1bd9b411bb0952542a6156cc2.png)
Daqui:
![\left[ cosx + (-1) \right] ^2 = 0 \left[ cosx + (-1) \right] ^2 = 0](/latexrender/pictures/021ddaf8323a9a649f637f9fbdd97c3f.png)
![\left[ cosx + (-1) \right] \cdot \left[ cosx + (-1) \right] = 0 \left[ cosx + (-1) \right] \cdot \left[ cosx + (-1) \right] = 0](/latexrender/pictures/c3cb79a73fb071969b25457e9881a90a.png)
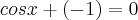
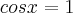
Agora, cuidado, antes de analisarmos a condição da raiz do enunciado, assim como o intervalo, temos que determinar a solução geral:
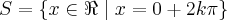
, sendo
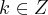
.
Somente agora, como o enunciado limita o intervalo em
![\left[ 0, 2\pi \right] \left[ 0, 2\pi \right]](/latexrender/pictures/c2929f82eed79c4c067a318f82b109a4.png)
, necessariamente,

e então obtemos a maior raiz

:

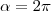
E o final, você já fez:
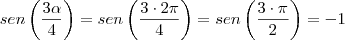
Espero ter ajudado!
![\left[0;2\pi \right] \left[0;2\pi \right]](/latexrender/pictures/2cdea0b108613b447c2f7d850fc61249.png) , se
, se  é a maior raiz da equação, então
é a maior raiz da equação, então 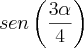 vale:
vale: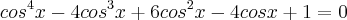
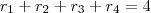
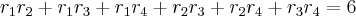
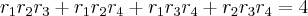
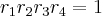
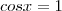 é:
é: 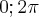
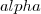 é a maior raiz, então é
é a maior raiz, então é 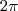
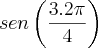
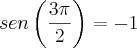
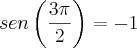


 ,
,  ,
,  ,
,  e
e  os coeficientes da equação:
os coeficientes da equação: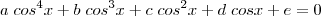





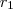 ,
, 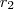 ,
, 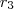 e
e 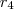 , as relações serão:
, as relações serão: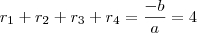
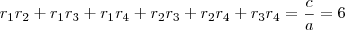
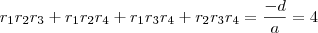
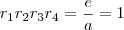


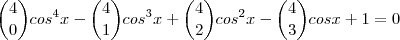
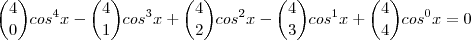
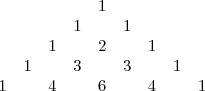
 , veja:
, veja: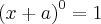

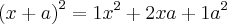
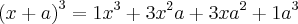
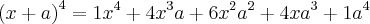
 .
.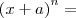
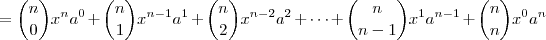
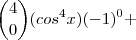
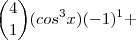
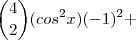
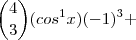
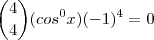
![\left[ cosx + (-1) \right] ^4 = 0 \left[ cosx + (-1) \right] ^4 = 0](/latexrender/pictures/6c53264e2db19b48a86fb1ed4dfb30c4.png)
![\left[ cosx + (-1) \right] ^2 \cdot \left[ cosx + (-1) \right] ^2 = 0 \left[ cosx + (-1) \right] ^2 \cdot \left[ cosx + (-1) \right] ^2 = 0](/latexrender/pictures/ee5e1ff1bd9b411bb0952542a6156cc2.png)
![\left[ cosx + (-1) \right] ^2 = 0 \left[ cosx + (-1) \right] ^2 = 0](/latexrender/pictures/021ddaf8323a9a649f637f9fbdd97c3f.png)
![\left[ cosx + (-1) \right] \cdot \left[ cosx + (-1) \right] = 0 \left[ cosx + (-1) \right] \cdot \left[ cosx + (-1) \right] = 0](/latexrender/pictures/c3cb79a73fb071969b25457e9881a90a.png)
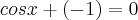
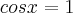
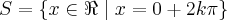 , sendo
, sendo 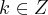 .
.![\left[ 0, 2\pi \right] \left[ 0, 2\pi \right]](/latexrender/pictures/c2929f82eed79c4c067a318f82b109a4.png) , necessariamente,
, necessariamente,  e então obtemos a maior raiz
e então obtemos a maior raiz