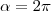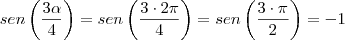por Ananda » Qua Mar 05, 2008 11:11
por Ananda » Qua Mar 05, 2008 11:11
Bom dia!
Eis o exercício:
Em ![\left[0;2\pi \right] \left[0;2\pi \right]](/latexrender/pictures/2cdea0b108613b447c2f7d850fc61249.png) , se
, se  é a maior raiz da equação, então
é a maior raiz da equação, então 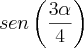 vale:
vale:
Resposta: -1
Como não consegui fazer a fatorial com o editor de fórmulas, anexei a equação.
Eu consegui chegar a resposta, mas creio que deve haver um método mais simples de se resolver...
Eu fiz assim:
- Resolvi as fatoriais, obtendo:
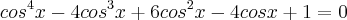
- Daí, usei as relações de Girardi e obtive:
I) 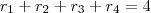
II) 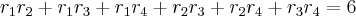
III) 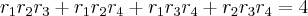
IV) 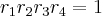
- Daí pelos valores possíveis de seno, o único valor que coresponde às expressões é 1.
E 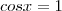 é:
é: 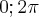
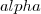 é a maior raiz, então é
é a maior raiz, então é 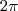
Substituindo:
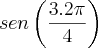
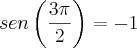
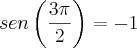
Grata desde já!
- Anexos
-
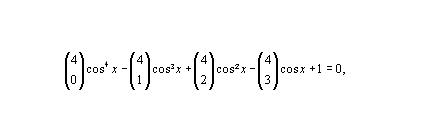
- imagem.JPG (4.88 KiB) Exibido 10354 vezes
Editado pela última vez por
Ananda em Sex Mar 07, 2008 12:20, em um total de 1 vez.
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qua Mar 05, 2008 15:24
por admin » Qua Mar 05, 2008 15:24
Olá, Ananda!
Primeiro, apenas um pequeno ajuste nas relações de Girard que você escreveu (provavelmente tenha sido um erro na edição):
Sendo

,

,

,

e

os coeficientes da equação:
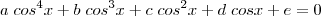





E as raízes
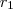
,
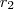
,
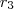
e
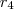
, as relações serão:
I)
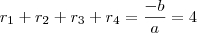
II)
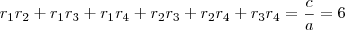
III)
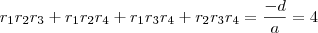
IV)
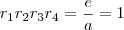
E sobre a sintaxe LaTeX dos números binomiais, você pode utilizar assim:
- Código: Selecionar todos
[tex]{n \choose p}[\tex]

Quanto ao outro método mais simples que você perguntou, vou escrever na próxima mensagem.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Qua Mar 05, 2008 16:22
por admin » Qua Mar 05, 2008 16:22
Ao olharmos esta equação:
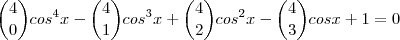
Os coeficientes lembram o triângulo de Pascal, veja:
Pois também pode ser escrita assim:
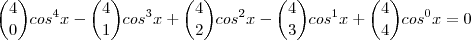
-Ou ainda, podemos lembrar dele após o desenvolvimento que você fez dos números binomiais, vendo os coeficientes na quinta linha:
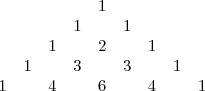
Um assunto relacionado é o desenvolvimento da potência n-ésima do binômio

, veja:
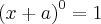

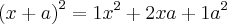
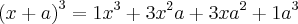
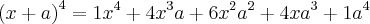
Note que os coeficientes de cada desenvolvimento formam a linha do triângulo de Pascal, sendo o número da linha igual ao expoente de

.
É a chamada
identidade do binômio de Newton:
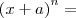
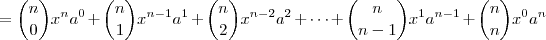
Então, podemos identificar esta identidade na equação dada para simplificá-la.
Para isso, ela ainda pode ser convenientemente reescrita assim:
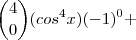
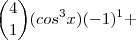
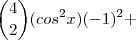
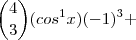
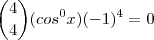
Portanto, agora a potência do binômio de Newton (antes do desenvolvimento) fica mais evidente, simplificando nossa equação, veja:
![\left[ cosx + (-1) \right] ^4 = 0 \left[ cosx + (-1) \right] ^4 = 0](/latexrender/pictures/6c53264e2db19b48a86fb1ed4dfb30c4.png)
Vamos então resolvê-la:
![\left[ cosx + (-1) \right] ^2 \cdot \left[ cosx + (-1) \right] ^2 = 0 \left[ cosx + (-1) \right] ^2 \cdot \left[ cosx + (-1) \right] ^2 = 0](/latexrender/pictures/ee5e1ff1bd9b411bb0952542a6156cc2.png)
Daqui:
![\left[ cosx + (-1) \right] ^2 = 0 \left[ cosx + (-1) \right] ^2 = 0](/latexrender/pictures/021ddaf8323a9a649f637f9fbdd97c3f.png)
![\left[ cosx + (-1) \right] \cdot \left[ cosx + (-1) \right] = 0 \left[ cosx + (-1) \right] \cdot \left[ cosx + (-1) \right] = 0](/latexrender/pictures/c3cb79a73fb071969b25457e9881a90a.png)
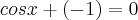
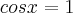
Agora, cuidado, antes de analisarmos a condição da raiz do enunciado, assim como o intervalo, temos que determinar a solução geral:
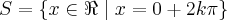
, sendo
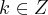
.
Somente agora, como o enunciado limita o intervalo em
![\left[ 0, 2\pi \right] \left[ 0, 2\pi \right]](/latexrender/pictures/c2929f82eed79c4c067a318f82b109a4.png)
, necessariamente,

e então obtemos a maior raiz

:

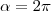
E o final, você já fez:
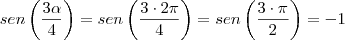
Espero ter ajudado!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Qua Mar 05, 2008 16:27
por Ananda » Qua Mar 05, 2008 16:27
Grata!
Ajudaste sim!
Estou tendo um pouco de problema com equações trigonométricas, porque fazendo de um modo dá uma resposta e fazendo de outro dá várias!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Qua Mar 05, 2008 16:49
por admin » Qua Mar 05, 2008 16:49
Por nada, Ananda.
Quanto ao "melhor" modo de se resolver um exercício, depende mais da preferência de quem resolve.
É claro que há formalidades na resolução, mas estou citando apenas o objetivo final.
Sobre as equações trigonométricas, em geral, quase todas podem ser reduzidas a uma destas três equações:



São as chamadas equações fundamentais.
Então, sugiro revisar bem a resolução destas equações, antes de qualquer outra mais complicada.
Eu fiz destaque na mensagem anterior sobre o conjunto-solução, pois é importante.
Nas funções circulares, temos infinitas soluções, pois o
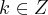
fará as "voltas" no círculo e a sentença da solução geral ainda será verdadeira (sentido horário ou anti-horário).
Há casos em que o intervalo é limitado, como no enunciado. Mas devemos fazer esta análise após encontrarmos o conjunto-verdade.
Bons estudos!
Quando precisar, escreva. Ajudarei se puder.
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (Mackenzie)
por my2009 » Sex Jan 28, 2011 21:28
- 1 Respostas
- 2686 Exibições
- Última mensagem por 0 kelvin

Sáb Jan 29, 2011 18:57
Logaritmos
-
- (Mackenzie) P.A. com P.G.
por Rafael16 » Sáb Ago 04, 2012 14:19
- 3 Respostas
- 10069 Exibições
- Última mensagem por MarceloFantini

Qui Set 13, 2012 10:20
Progressões
-
- Mackenzie
por Maria Livia » Qua Fev 27, 2013 22:29
- 1 Respostas
- 33665 Exibições
- Última mensagem por Cleyson007

Qua Fev 27, 2013 22:41
Geometria Espacial
-
- (MACKENZIE-SP)
por Thiago 86 » Qua Mar 27, 2013 23:23
- 4 Respostas
- 3201 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 06, 2013 21:03
Inequações
-
- Questão (MACKENZIE)
por Carolziiinhaaah » Qua Jun 16, 2010 12:04
- 1 Respostas
- 3444 Exibições
- Última mensagem por Elcioschin

Qua Jun 16, 2010 13:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left[0;2\pi \right] \left[0;2\pi \right]](/latexrender/pictures/2cdea0b108613b447c2f7d850fc61249.png) , se
, se  é a maior raiz da equação, então
é a maior raiz da equação, então 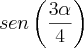 vale:
vale: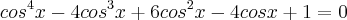
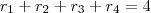
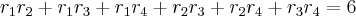
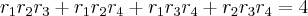
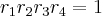
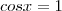 é:
é: 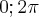
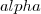 é a maior raiz, então é
é a maior raiz, então é 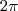
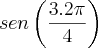
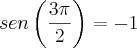
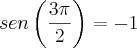


 ,
,  ,
,  ,
,  e
e  os coeficientes da equação:
os coeficientes da equação: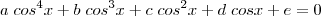





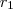 ,
, 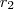 ,
, 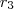 e
e 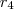 , as relações serão:
, as relações serão: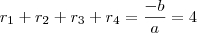
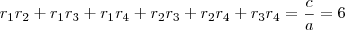
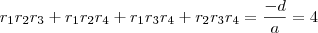
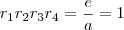


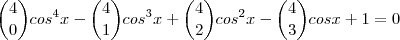
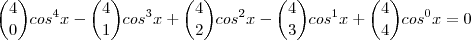
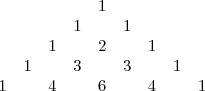
 , veja:
, veja: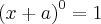

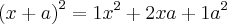
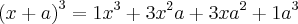
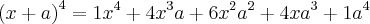
 .
.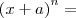
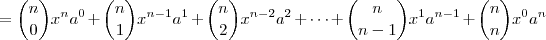
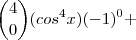
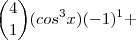
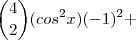
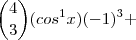
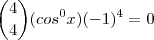
![\left[ cosx + (-1) \right] ^4 = 0 \left[ cosx + (-1) \right] ^4 = 0](/latexrender/pictures/6c53264e2db19b48a86fb1ed4dfb30c4.png)
![\left[ cosx + (-1) \right] ^2 \cdot \left[ cosx + (-1) \right] ^2 = 0 \left[ cosx + (-1) \right] ^2 \cdot \left[ cosx + (-1) \right] ^2 = 0](/latexrender/pictures/ee5e1ff1bd9b411bb0952542a6156cc2.png)
![\left[ cosx + (-1) \right] ^2 = 0 \left[ cosx + (-1) \right] ^2 = 0](/latexrender/pictures/021ddaf8323a9a649f637f9fbdd97c3f.png)
![\left[ cosx + (-1) \right] \cdot \left[ cosx + (-1) \right] = 0 \left[ cosx + (-1) \right] \cdot \left[ cosx + (-1) \right] = 0](/latexrender/pictures/c3cb79a73fb071969b25457e9881a90a.png)
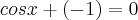
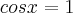
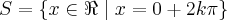 , sendo
, sendo 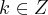 .
.![\left[ 0, 2\pi \right] \left[ 0, 2\pi \right]](/latexrender/pictures/c2929f82eed79c4c067a318f82b109a4.png) , necessariamente,
, necessariamente,  e então obtemos a maior raiz
e então obtemos a maior raiz