 por klysman » Qui Mai 03, 2012 20:12
por klysman » Qui Mai 03, 2012 20:12
gente , nao to conseguindo resolver essa formula
alguem pode me explicar por favor
é urgente, tenho que entregar meu trabalho escolar amanha =/
Função ate onde eu fui
B=(Xp,0) A(-2,1) Dent= Raiz quadrada de 10
( Xp,-(-2) )²+ (0,-1)² =Raiz de 10
(Xp,2)² + 1 = Raiz de 10
....
a parti dai não sei mais oqui fazer , é como chegar a resposta !
Alguem me ajuda por favor
Obrigado . =]
-
klysman
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mai 01, 2012 20:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matematica
- Andamento: cursando
 por Russman » Qui Mai 03, 2012 20:47
por Russman » Qui Mai 03, 2012 20:47
.
Editado pela última vez por
Russman em Qui Mai 03, 2012 20:54, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Qui Mai 03, 2012 20:53
por Russman » Qui Mai 03, 2012 20:53
Eu não entendi muito beem oque você precisa calcular. Por que você não posta o problema completo? Acho que fica melhor de te ajudar.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por klysman » Qui Mai 03, 2012 20:55
por klysman » Qui Mai 03, 2012 20:55

Esse e um problema da Geometria analitica , usando o teorema de pitagoras
só qui não to sabendo tira essa 10 da Raiz
Deu pra intender direitinho ? Obg
-
klysman
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mai 01, 2012 20:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matematica
- Andamento: cursando
 por Russman » Qui Mai 03, 2012 21:10
por Russman » Qui Mai 03, 2012 21:10
Nessa equação o
![\sqrt[]{10} \sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png)
não é ao quadrado? Porque então fica
![{(x+2)}^{2} + 1 = {(\sqrt[]{10})}^{2} {(x+2)}^{2} + 1 = {(\sqrt[]{10})}^{2}](/latexrender/pictures/0b0fd41a31b6c1c15c7f4b1f17377d05.png)
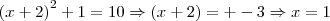
ou

.
Lembre-se que no Teorema de Pitágoras todos os termos são elevados ao quadrado.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por klysman » Qui Mai 03, 2012 21:12
por klysman » Qui Mai 03, 2012 21:12
Obrigado , entendi ^^
-
klysman
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Mai 01, 2012 20:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matematica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7466 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4151 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Como resolver raiz dentro de raiz ?
 por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
- 10 Respostas
- 13803 Exibições
- Última mensagem por LuizAquino

Sex Ago 24, 2012 07:50
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2246 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- [Radiciação] Raiz dentro de raiz
por amandasousa_m » Sex Jul 19, 2013 09:37
- 2 Respostas
- 3445 Exibições
- Última mensagem por amandasousa_m

Sex Jul 19, 2013 21:58
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![\sqrt[]{10} \sqrt[]{10}](/latexrender/pictures/471a3f5071e0c768f7370dfae6de7f4a.png) não é ao quadrado? Porque então fica
não é ao quadrado? Porque então fica![{(x+2)}^{2} + 1 = {(\sqrt[]{10})}^{2} {(x+2)}^{2} + 1 = {(\sqrt[]{10})}^{2}](/latexrender/pictures/0b0fd41a31b6c1c15c7f4b1f17377d05.png)
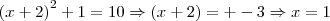 ou
ou  .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
