 por Cleyson007 » Qui Mai 03, 2012 09:54
por Cleyson007 » Qui Mai 03, 2012 09:54
Bom dia a todos!
Calcule a integral iterada
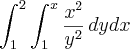
Posso fazer isso?
![\int_{1}^{2}\left [\frac{x^2y}{\frac{y^3}{3}} \right ]_{1}^{x}dx\Rightarrow \int_{1}^{2}\left [ \frac{3x^2y}{y^3} \right ]_{1}^{x}dx \int_{1}^{2}\left [\frac{x^2y}{\frac{y^3}{3}} \right ]_{1}^{x}dx\Rightarrow \int_{1}^{2}\left [ \frac{3x^2y}{y^3} \right ]_{1}^{x}dx](/latexrender/pictures/a75fec1df3f47749a5f45d83bae82944.png)
Se alguém puder me ajudar..
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Cleyson007 » Qui Mai 03, 2012 12:22
por Cleyson007 » Qui Mai 03, 2012 12:22
Bom dia Luiz Aquino!
![\int_{1}^{2}\left [- \frac{x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow\int_{1}^{2}-({x}^{2}{y}^{-1})\,dx \int_{1}^{2}\left [- \frac{x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow\int_{1}^{2}-({x}^{2}{y}^{-1})\,dx](/latexrender/pictures/655a42fd8e3091e8a838964cc04c87ef.png)
Estou indo no caminho certo?
![\left [-\left ( \frac{x^{3}}{3}\left ( \frac{1}{y} \right ) \right ) \right ]_{1}^{2}\Rightarrow \left [ -\left ( \frac{x^{3}}{3y} \right ) \right ]_{1}^{2} \left [-\left ( \frac{x^{3}}{3}\left ( \frac{1}{y} \right ) \right ) \right ]_{1}^{2}\Rightarrow \left [ -\left ( \frac{x^{3}}{3y} \right ) \right ]_{1}^{2}](/latexrender/pictures/aeb52c371e1df2db7d55fecbd2e13491.png)
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Qui Mai 03, 2012 13:37
por LuizAquino » Qui Mai 03, 2012 13:37
Cleyson007 escreveu:![\int_{1}^{2}\left [- \frac{x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow\int_{1}^{2}-({x}^{2}{y}^{-1})\,dx \int_{1}^{2}\left [- \frac{x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow\int_{1}^{2}-({x}^{2}{y}^{-1})\,dx](/latexrender/pictures/655a42fd8e3091e8a838964cc04c87ef.png)
Estou indo no caminho certo?
![\left [-\left ( \frac{x^{3}}{3}\left ( \frac{1}{y} \right ) \right ) \right ]_{1}^{2}\Rightarrow \left [ -\left ( \frac{x^{3}}{3y} \right ) \right ]_{1}^{2} \left [-\left ( \frac{x^{3}}{3}\left ( \frac{1}{y} \right ) \right ) \right ]_{1}^{2}\Rightarrow \left [ -\left ( \frac{x^{3}}{3y} \right ) \right ]_{1}^{2}](/latexrender/pictures/aeb52c371e1df2db7d55fecbd2e13491.png)
Você está errado. O correto seria:
![\int_{1}^{2}\left[-\frac{x^2}{y}\right]_1^x\,dx = \int_{1}^{2}\left[\left(-\frac{x^2}{x}\right) -\left( -\frac{x^2}{1}\right)\right]\,dx = \int_{1}^{2} -x + x^2\right)\,dx \int_{1}^{2}\left[-\frac{x^2}{y}\right]_1^x\,dx = \int_{1}^{2}\left[\left(-\frac{x^2}{x}\right) -\left( -\frac{x^2}{1}\right)\right]\,dx = \int_{1}^{2} -x + x^2\right)\,dx](/latexrender/pictures/944e36dfd1f56796108bbfa3950bdfd2.png)
Agora termine o exercício a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Cleyson007 » Qui Mai 03, 2012 15:32
por Cleyson007 » Qui Mai 03, 2012 15:32
Boa tarde Luiz Aquino!
Luiz, eu podia jurar que estava correto nessa passagem
![\int_{1}^{2}\left [ \frac{-x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow \int_{1}^{2}-(x^{2}y^{-1})\,dx \int_{1}^{2}\left [ \frac{-x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow \int_{1}^{2}-(x^{2}y^{-1})\,dx](/latexrender/pictures/e7a695209c413b2aafc8bf2b6ea32f2a.png)
Para mim o lado esquerdo é igual ao direito. Gostaria de saber por que está errado..
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por LuizAquino » Qui Mai 03, 2012 16:20
por LuizAquino » Qui Mai 03, 2012 16:20
Cleyson007 escreveu:Luiz, eu podia jurar que estava correto nessa passagem
![\int_{1}^{2}\left [ \frac{-x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow \int_{1}^{2}-(x^{2}y^{-1})\,dx \int_{1}^{2}\left [ \frac{-x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow \int_{1}^{2}-(x^{2}y^{-1})\,dx](/latexrender/pictures/e7a695209c413b2aafc8bf2b6ea32f2a.png)
Para mim o lado esquerdo é igual ao direito. Gostaria de saber por que está errado..
O correto seria escrever:
![\int_{1}^{2}\left[\frac{-x^2}{y} \right]_{1}^{x}\,dx = \int_{1}^{2}\left[-x^{2}y^{-1} \right]_1^x\,dx \int_{1}^{2}\left[\frac{-x^2}{y} \right]_{1}^{x}\,dx = \int_{1}^{2}\left[-x^{2}y^{-1} \right]_1^x\,dx](/latexrender/pictures/97971325f33a81b2bbdd2f464c73401f.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como posso resolver isso????
por Mimizinha » Qui Mar 20, 2008 10:15
- 6 Respostas
- 6581 Exibições
- Última mensagem por Mimizinha

Qui Mar 20, 2008 13:15
Geometria Analítica
-
- [derivadas] como posso simplificar isso?
por vinicastro » Dom Dez 16, 2012 21:09
- 1 Respostas
- 1601 Exibições
- Última mensagem por e8group

Seg Dez 17, 2012 07:50
Cálculo: Limites, Derivadas e Integrais
-
- Sem usar a fórmula de Herao como posso fazer
 por zenildo » Qui Jun 09, 2016 18:38
por zenildo » Qui Jun 09, 2016 18:38
- 1 Respostas
- 1956 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 11, 2016 09:07
Geometria Analítica
-
- Posso usar logaritmo para fazer essa conta..
por guitaedis » Ter Nov 30, 2010 18:42
- 0 Respostas
- 2121 Exibições
- Última mensagem por guitaedis

Ter Nov 30, 2010 18:42
Matemática Financeira
-
- Figura Geométrica (Alguém tem o poder de fazer isso?)
por Balanar » Qui Set 02, 2010 04:07
- 0 Respostas
- 906 Exibições
- Última mensagem por Balanar

Qui Set 02, 2010 04:07
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
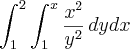
![\int_{1}^{2}\left [\frac{x^2y}{\frac{y^3}{3}} \right ]_{1}^{x}dx\Rightarrow \int_{1}^{2}\left [ \frac{3x^2y}{y^3} \right ]_{1}^{x}dx \int_{1}^{2}\left [\frac{x^2y}{\frac{y^3}{3}} \right ]_{1}^{x}dx\Rightarrow \int_{1}^{2}\left [ \frac{3x^2y}{y^3} \right ]_{1}^{x}dx](/latexrender/pictures/a75fec1df3f47749a5f45d83bae82944.png)

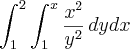
![\int_{1}^{2}\left [\frac{x^2y}{\frac{y^3}{3}} \right ]_{1}^{x}dx\Rightarrow \int_{1}^{2}\left [ \frac{3x^2y}{y^3} \right ]_{1}^{x}dx \int_{1}^{2}\left [\frac{x^2y}{\frac{y^3}{3}} \right ]_{1}^{x}dx\Rightarrow \int_{1}^{2}\left [ \frac{3x^2y}{y^3} \right ]_{1}^{x}dx](/latexrender/pictures/a75fec1df3f47749a5f45d83bae82944.png)


![= \int_{1}^{2}\left[x^2\frac{y^{-2 + 1}}{-2 + 1}\right]_1^x\,dx = \int_{1}^{2}\left[x^2\frac{y^{-2 + 1}}{-2 + 1}\right]_1^x\,dx](/latexrender/pictures/ad76072ccdbeb6ff6049b2a8ef112a6e.png)
![= \int_{1}^{2}\left[-\frac{x^2}{y}\right]_1^x\,dx = \int_{1}^{2}\left[-\frac{x^2}{y}\right]_1^x\,dx](/latexrender/pictures/cb833adf06a3c806f072c276b4afe3b0.png)

![\int_{1}^{2}\left [- \frac{x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow\int_{1}^{2}-({x}^{2}{y}^{-1})\,dx \int_{1}^{2}\left [- \frac{x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow\int_{1}^{2}-({x}^{2}{y}^{-1})\,dx](/latexrender/pictures/655a42fd8e3091e8a838964cc04c87ef.png)
![\left [-\left ( \frac{x^{3}}{3}\left ( \frac{1}{y} \right ) \right ) \right ]_{1}^{2}\Rightarrow \left [ -\left ( \frac{x^{3}}{3y} \right ) \right ]_{1}^{2} \left [-\left ( \frac{x^{3}}{3}\left ( \frac{1}{y} \right ) \right ) \right ]_{1}^{2}\Rightarrow \left [ -\left ( \frac{x^{3}}{3y} \right ) \right ]_{1}^{2}](/latexrender/pictures/aeb52c371e1df2db7d55fecbd2e13491.png)

![\int_{1}^{2}\left[-\frac{x^2}{y}\right]_1^x\,dx = \int_{1}^{2}\left[\left(-\frac{x^2}{x}\right) -\left( -\frac{x^2}{1}\right)\right]\,dx = \int_{1}^{2} -x + x^2\right)\,dx \int_{1}^{2}\left[-\frac{x^2}{y}\right]_1^x\,dx = \int_{1}^{2}\left[\left(-\frac{x^2}{x}\right) -\left( -\frac{x^2}{1}\right)\right]\,dx = \int_{1}^{2} -x + x^2\right)\,dx](/latexrender/pictures/944e36dfd1f56796108bbfa3950bdfd2.png)

![\int_{1}^{2}\left [ \frac{-x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow \int_{1}^{2}-(x^{2}y^{-1})\,dx \int_{1}^{2}\left [ \frac{-x^2}{y} \right ]_{1}^{x}\,dx\Rightarrow \int_{1}^{2}-(x^{2}y^{-1})\,dx](/latexrender/pictures/e7a695209c413b2aafc8bf2b6ea32f2a.png)

![\int_{1}^{2}\left[\frac{-x^2}{y} \right]_{1}^{x}\,dx = \int_{1}^{2}\left[-x^{2}y^{-1} \right]_1^x\,dx \int_{1}^{2}\left[\frac{-x^2}{y} \right]_{1}^{x}\,dx = \int_{1}^{2}\left[-x^{2}y^{-1} \right]_1^x\,dx](/latexrender/pictures/97971325f33a81b2bbdd2f464c73401f.png)
