É conhecido e fácilmente provado/verificado que o lugar geométrico que dista o mesmo de um certo ponto é a circunferência. Assim, os pontos do conjunto C são tais que

.
Ou ainda,
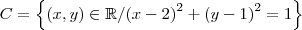
.
Para resolver este problema temos de calcular qual ,ou quais, pontos da reta
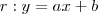
, que adimite os pontos (3,2) e (8,7), são também admitidos por C. Isto é, devemos solucionar o sistema

Vamos primeiro identificar a reta r. Para tanto basta calcular a e b tais que
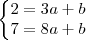
A solução é

e

.Portanto,
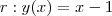
.
Assim, o sistema se torna
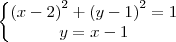
e é facilmente solucionado substituindo-se y da 1° eq. pela da segunda. Os dois pontos solução são a intersecção entre

e

.

.


 .
.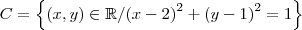 .
.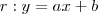 , que adimite os pontos (3,2) e (8,7), são também admitidos por C. Isto é, devemos solucionar o sistema
, que adimite os pontos (3,2) e (8,7), são também admitidos por C. Isto é, devemos solucionar o sistema
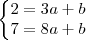
 e
e  .Portanto,
.Portanto, 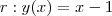 .
.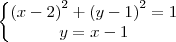
 e
e  .
. .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.