 por LuizCarlos » Ter Mai 01, 2012 22:12
por LuizCarlos » Ter Mai 01, 2012 22:12
Olá amigos professores, boa noite!
Estou encontrando dificuldade para resolver esse problema de regra de três!
Com uma certa quantidade de fio, uma fábrica produz
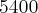
m de tecido com

cm de largura em
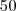
minutos. Quantos metros de tecido, com

m e
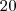
cm de largura, seriam produzidos em
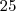
minutos.
A minha resposta está sendo
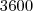
m de tecido.
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por DanielFerreira » Ter Mai 01, 2012 22:30
por DanielFerreira » Ter Mai 01, 2012 22:30
5400m ----------------- 90cm (largura) ---------------------- 50min.
? ------------------------ 120cm (100 + 20) ------------------ 25min.
___________________(dir.)________________________(dir.)

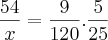
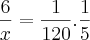

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por LuizCarlos » Ter Mai 01, 2012 22:57
por LuizCarlos » Ter Mai 01, 2012 22:57
danjr5 escreveu:5400m ----------------- 90cm (largura) ---------------------- 50min.
? ------------------------ 120cm (100 + 20) ------------------ 25min.
___________________(dir.)________________________(dir.)

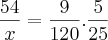
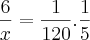

Olá dnjr5 meu brother, tranquilo.
Estou resolvendo dessa forma, mas a resposta no livro é:

m, será que o livro está errado.
Obrigado por me ajudar!
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por DanielFerreira » Qua Mai 02, 2012 00:48
por DanielFerreira » Qua Mai 02, 2012 00:48
Desculpe o equívoco!
Segue o raciocínio:
Se com 90cm de largura se produz um tecido com 5400m; com 120cm, ele será menor (a quantidade de fio é a mesma, por isso!)
danjr5 escreveu:5400m ----------------- 90cm (largura) ---------------------- 50min.
? ------------------------ 120cm (100 + 20) ------------------ 25min.
___________________(inv.)________________________(dir.)
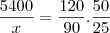


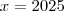
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema! regra de três composta
por LuizCarlos » Qui Abr 12, 2012 17:59
- 1 Respostas
- 2355 Exibições
- Última mensagem por MarceloFantini

Qui Abr 12, 2012 19:33
Álgebra Elementar
-
- regra de tres composta
por Liliani » Qui Mar 18, 2010 16:35
- 2 Respostas
- 5609 Exibições
- Última mensagem por Liliani

Qua Mar 31, 2010 17:23
Pedidos
-
- Regra de três composta
por Danilo Dias Vilela » Qua Ago 25, 2010 11:44
- 0 Respostas
- 1897 Exibições
- Última mensagem por Danilo Dias Vilela

Qua Ago 25, 2010 11:44
Álgebra Elementar
-
- regra de três composta
por hevhoram » Dom Mai 22, 2011 22:07
- 1 Respostas
- 2558 Exibições
- Última mensagem por Molina

Seg Mai 23, 2011 00:59
Álgebra Elementar
-
- regra de tres composta
por alissonade » Sex Ago 03, 2012 14:01
- 2 Respostas
- 2565 Exibições
- Última mensagem por alissonade

Sáb Ago 04, 2012 00:52
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
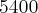 m de tecido com
m de tecido com  cm de largura em
cm de largura em 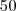 minutos. Quantos metros de tecido, com
minutos. Quantos metros de tecido, com  m e
m e 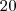 cm de largura, seriam produzidos em
cm de largura, seriam produzidos em 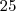 minutos.
minutos.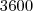 m de tecido.
m de tecido.


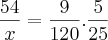
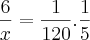


 m, será que o livro está errado.
m, será que o livro está errado.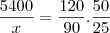


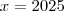

 .
.



