Uma equação do terceiro grau é uma função polinomial com 3 raízes. É preciso encontrar as três raízes, que é o lugar onde a função toca o eixo x (pode existir duas, uma ou nenhuma raíz).
Depois disso, é muito bom esboçar o gráfico da derivada dessa função (embora não seja preciso), pois ele te garante em quais valores a função do 3º grau está crescendo e em quais ela está decrescendo. (Em valores positivos da derivada, a função está crescendo, em valores negativos, decrescendo).
Exemplo:
Seja a inequação :
x³ - 2x² - x + 1 > -1
x³ - 2x² - x + 2 > 0
x²(x - 2) - (x - 2) > 0
(x² - 1)(x - 2) > 0
(x + 1)(x - 1)(x - 2) > 0
Sabemos que as raízes são -1 ; 1 ; 2, mas não sabemos em quais intervalos a função é positiva ou negativa. Ao invéz de olhar a derivada, façamos algo mais lógico:
O primeiro dos números (seguindo a ordem do plano cartesiano) que zera a função é o x = -1. Antes dele, observamos que as funções possuíam valores negarivos, pois (x + 1) era negativo, (x - 1) também e (x - 2) também (- - - = -). Agora, depois de x = -1, teremos:
+ - - = +
Até que cheguemos em x = 1, onde a situação se torna:
+ + - = -
Até atingirmos x = 2, onde teremos:
+ + + = +
Portanto, podemos afirmar:
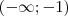
--> Negativa

--> Positiva

---> Negativa

---> Positiva
Dessa forma, fica simples definir o conjunto solução:



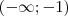 --> Negativa
--> Negativa --> Positiva
--> Positiva ---> Negativa
---> Negativa ---> Positiva
---> Positiva

