prestações, mensais e fixas, com juros efetivos de 24% ao ano. Qual o valor de cada
prestação a ser paga se a 1ª parcela vencer no dia da concessão do crédito e 30 dias
depois? Há diferença nesses valores? Por quê?
A fórmula de prestação postecipada é a seguinte:
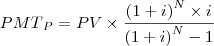 , certo?
, certo?Aprendi que o adequado é converter o tempo à taxa, por dar menos trabalho.
Convertendo (24 meses=2 anos), a fórmula fica assim:
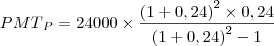
Fazendo essa álgebra, o meu resultado é:
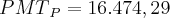
E quando utilizo a HP12C e aperto a seguinte sequência de teclas:
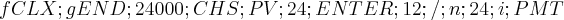 , o resultado é o mesmo:
, o resultado é o mesmo: 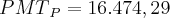
Acho que esse resultado é impróprio.
Em vez de converter o tempo, ao converter a taxa, a fórmula seria essa?
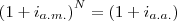
Se for, como resolvo?
Como não consegui, usei o inverso de potenciação (radiciação), que, a meu ver, seria assim:
![\sqrt[N]{\left(1+{i}_{a.a.} \right)}=\left(1+{i}_{a.m.} \right) \sqrt[N]{\left(1+{i}_{a.a.} \right)}=\left(1+{i}_{a.m.} \right)](/latexrender/pictures/64969e9152661e3c99d2611e6562bb0e.png) ou
ou 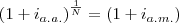 , está certo?
, está certo?Resolvendo com radiciação eu cheguei ao resultado:
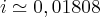 , ou seja, aproximadamente 1,81%.
, ou seja, aproximadamente 1,81%.Porém, ao resolver tanto pela álgebra como pela HP12C, o resultado é:

Por quê dá absurdamente diferente convertendo tanto o tempo quanto a taxa?
Onde estou errando?
Alguém pode me explicar?
O resto do exercício é basicamente a mesma coisa, pois pra achar o antecipado, preciso do postecipado, e sem isso fica impossível de saber.
Desde já, obrigado!




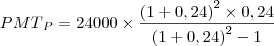

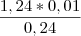 = 0,051666
= 0,051666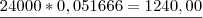
![\sqrt[12]{1,24} \sqrt[12]{1,24}](/latexrender/pictures/892c262c9d0653fba4b117776ded1a05.png)
![\sqrt[6]{1,24} \sqrt[6]{1,24}](/latexrender/pictures/3ffb1d90c1d2ca391a7b1030d12a347f.png)

 .
.



