 por ENG » Sáb Abr 28, 2012 04:09
por ENG » Sáb Abr 28, 2012 04:09
Olá. Estou estudando, através de um livro, o cálculo do coeficiente para uma serie trig. de Fourier de uma certa função. Lá tem um exemplo assim:
![{a}_{n}=\frac{2}{0,2}\int_{0}^{0,1}5.cos\,n\,{\omega}_{0}\,t\,dt=\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right] {a}_{n}=\frac{2}{0,2}\int_{0}^{0,1}5.cos\,n\,{\omega}_{0}\,t\,dt=\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right]](/latexrender/pictures/65d97eb477c1c24ad8ec4751f86a99eb.png)
e a solução do exemplo continua...
O trecho no qual está minha dúvida é a última parte da expressão( teria que colocar os limites 0 e 0,1 nos colchetes mas não consegui):
![\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right] \left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right]](/latexrender/pictures/c1c7a6ac6c4b516f8a3b1b3eb26100d8.png)
Sei que
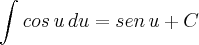
, mas como surgiu
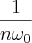
?
-
ENG
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Abr 28, 2012 03:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Sáb Abr 28, 2012 04:48
por Russman » Sáb Abr 28, 2012 04:48
Pense na função
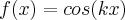
, onde

é uma constante real.
Se vc integrar esta função com ralação a

terá de apelar para uma substituição, a fim de tomar o integrando como
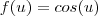
. Veja, tomando
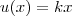
temos então
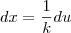
e , portanto,
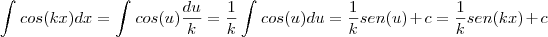
.
A sua integral é com relação a

e não
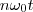
.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] integral - cosseno
por beel » Dom Nov 20, 2011 23:10
- 1 Respostas
- 1064 Exibições
- Última mensagem por LuizAquino

Dom Nov 20, 2011 23:26
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4348 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3684 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 3077 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2501 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{a}_{n}=\frac{2}{0,2}\int_{0}^{0,1}5.cos\,n\,{\omega}_{0}\,t\,dt=\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right] {a}_{n}=\frac{2}{0,2}\int_{0}^{0,1}5.cos\,n\,{\omega}_{0}\,t\,dt=\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right]](/latexrender/pictures/65d97eb477c1c24ad8ec4751f86a99eb.png) e a solução do exemplo continua...
e a solução do exemplo continua...![\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right] \left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right]](/latexrender/pictures/c1c7a6ac6c4b516f8a3b1b3eb26100d8.png)
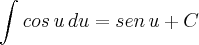 , mas como surgiu
, mas como surgiu 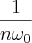 ?
?
![{a}_{n}=\frac{2}{0,2}\int_{0}^{0,1}5.cos\,n\,{\omega}_{0}\,t\,dt=\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right] {a}_{n}=\frac{2}{0,2}\int_{0}^{0,1}5.cos\,n\,{\omega}_{0}\,t\,dt=\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right]](/latexrender/pictures/65d97eb477c1c24ad8ec4751f86a99eb.png) e a solução do exemplo continua...
e a solução do exemplo continua...![\left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right] \left[\frac{2 \ast 5}{0,2}.\frac{1}{n{\omega}_{0}}sen\,n\, {\omega}_{0}\,t \right]](/latexrender/pictures/c1c7a6ac6c4b516f8a3b1b3eb26100d8.png)
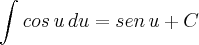 , mas como surgiu
, mas como surgiu 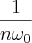 ?
?
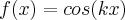 , onde
, onde  é uma constante real.
é uma constante real. terá de apelar para uma substituição, a fim de tomar o integrando como
terá de apelar para uma substituição, a fim de tomar o integrando como 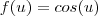 . Veja, tomando
. Veja, tomando 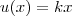 temos então
temos então 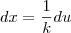 e , portanto,
e , portanto,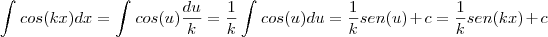 .
. e não
e não 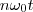 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.