 por regiamartina12 » Qui Abr 26, 2012 11:30
por regiamartina12 » Qui Abr 26, 2012 11:30
Estou tendo dúvidas no conceito de geometria plana, acho que por isso que não estou conseguindo.
[b]a) Quantas retas são determinadas por 7 pontos coplanares, dos quais 3 estão em linha reta? Resposta 19
a
C7,3 = 7!__
3! (7-3)!
C7,3 = 7!__
3.2 4!
C7,3 = 7.6.5__ = 35
6
-
regiamartina12
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Abr 25, 2012 16:22
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: ADMINISTRAÇÃO
- Andamento: cursando
 por DanielFerreira » Dom Abr 29, 2012 16:30
por DanielFerreira » Dom Abr 29, 2012 16:30
regiamartina12 escreveu:Estou tendo dúvidas no conceito de geometria plana, acho que por isso que não estou conseguindo.
a) Quantas retas são determinadas por 7 pontos coplanares, dos quais 3 estão em linha reta? Resposta 19


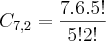
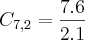


Imagine que os três pontos alinhados sejam A, B e C.
Temos que AB, BC e AC representam a mesma reta, por isso devemos desconsiderar duas delas.
21 - 2 =
[b]19"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Combinação de Numeros]Combinação até chegar em outro
por moacirrf » Dom Set 30, 2012 15:51
- 0 Respostas
- 1785 Exibições
- Última mensagem por moacirrf

Dom Set 30, 2012 15:51
Análise Combinatória
-
- AREAS DE FIGURAS
por JOHNY » Qui Set 02, 2010 18:17
- 1 Respostas
- 1966 Exibições
- Última mensagem por Douglasm

Qui Set 02, 2010 18:48
Geometria Plana
-
- Progressões Geométricas
por Anderson Alves » Ter Abr 24, 2012 23:08
- 2 Respostas
- 1536 Exibições
- Última mensagem por Russman

Qua Abr 25, 2012 20:00
Progressões
-
- Progressões Geométricas
por Anderson Alves » Sáb Abr 28, 2012 20:47
- 1 Respostas
- 2311 Exibições
- Última mensagem por DanielFerreira

Dom Abr 29, 2012 15:45
Progressões
-
- Conjunto de Figuras Planas
por gustavowelp » Qua Jun 30, 2010 15:37
- 4 Respostas
- 4342 Exibições
- Última mensagem por gustavowelp

Qua Jun 30, 2010 17:44
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




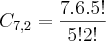
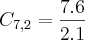




 .
.



