3 lim? ln?|x-3| - 2 lim ?ln?|x+4|
x?? x??
Alguém sabe me explicar por que essa integral é igual a ? ?



Ewerton Farias escreveu:3 lim? ln?|x-3| - 2 lim ?ln?|x+4|
x?? x??
Alguém sabe me explicar por que essa integral é igual a ? ?

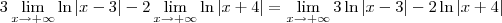

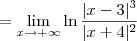

 , temos que:
, temos que: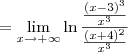
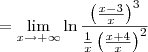

 e que
e que  vai para 1. Isso significa que dentro da função ln temos uma expressão que vai para
vai para 1. Isso significa que dentro da função ln temos uma expressão que vai para 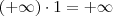 .
.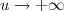 , então
, então 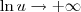 . Em outras palavras, se o que está "dentro" da função ln vai para
. Em outras palavras, se o que está "dentro" da função ln vai para  , então o valor da função ln vai para
, então o valor da função ln vai para  também.
também.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

