[x² - 5x + 6] / [x² - x + 42] >= 0
Restrições:
[x² - x + 42] tem que ser diferente de zero.
Delta = b² - 4 . a . c
Delta = (-1)² - 4 . 1 . 42
Delta = 1 - 168
Delta = - 167
Como delta é negativo não existe raiz real. Como o valor de a é positivo a concavidade da parábola é voltada para cima. Portanto, qualquer que seja o valor de x sempre teremos um valor positivo (e nunca será zero) para esta função.
Como sabemos que a função da parte de baixo da fração sempre será positiva, e que quando dividimos a parte de cima pela de baixo temos que ter um valor igual ou maior que zero, significa que a função de cima, pode resultar em zero ou ser um valor positivo, pois, se for negativo vem a regra de sinal e teríamos um resultano menor que zero.
Então, calculemos a função de cima x² - 5x + 6 = 0, e verificamos o estudo dos sinais da mesma.
Delta = b² - 4 . a . c
Delta = (-5)² - 4 . 1 . 6
Delta = 25 - 24
Delta = 1
![\sqrt[]{\Delta} \sqrt[]{\Delta}](/latexrender/pictures/330b226b014cd1baae65efe339f0ec25.png)
= 1
x =
![\frac{-b +ou- \sqrt[]{\Delta} }{2a} \frac{-b +ou- \sqrt[]{\Delta} }{2a}](/latexrender/pictures/f4e2530cd4c1230260180adf2d64a4c9.png)
x =

x =

x' = (5 + 1) / 2 = 6/2 = 3
x" = (5 - 1) / 2 = 4/2 = 2
A função da parte de cima é igual a zero quando x = 2 ou x = 3.
Esta função também tem concavidade para cima pois a é positivo.
Os valores menores que 2 geram resultados positivos (mesmo que a), os valores entre 2 e 3 geram resultados negativos (contrário de a) e os valores maiores que 3 geram resultados positivos (mesmo que a).
Portanto,como a função de cima não pode ser negativa devemos excluir o intervalo em que ela tem resultados negativos que é do 2 ao 3.
Sendo assim, a solução do exercício fica:
![{ x \in \Re | (-\infty , 2] \cup [3 , +\infty) } { x \in \Re | (-\infty , 2] \cup [3 , +\infty) }](/latexrender/pictures/77fda2dce258fbdd3e0e84aa5c161777.png)
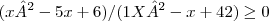
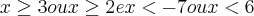

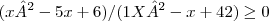
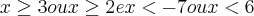



![\sqrt[]{\Delta} \sqrt[]{\Delta}](/latexrender/pictures/330b226b014cd1baae65efe339f0ec25.png) = 1
= 1![\frac{-b +ou- \sqrt[]{\Delta} }{2a} \frac{-b +ou- \sqrt[]{\Delta} }{2a}](/latexrender/pictures/f4e2530cd4c1230260180adf2d64a4c9.png)


![{ x \in \Re | (-\infty , 2] \cup [3 , +\infty) } { x \in \Re | (-\infty , 2] \cup [3 , +\infty) }](/latexrender/pictures/77fda2dce258fbdd3e0e84aa5c161777.png)



