 por Kabection » Seg Abr 16, 2012 23:40
por Kabection » Seg Abr 16, 2012 23:40
Olá, resolvendo uma questão sobre Derivadas me deparei com uma situação inusitada. Que é o seguinte: A questão pede para determinar a equação da reta tangente em (p,f(p)) de:
f(x)= sen(x)+cos(3x) ,
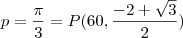
------------- f(p)=
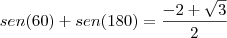
Resolvendo:

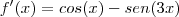
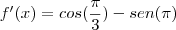
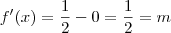
Para determinar a equação:

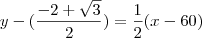

Mas testando pelo Geogebra, o resultado da equação da reta tangente em (p,f(p)) é:

Que consigo obter quando coloco o ponto P = (

, onde
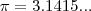
Então devo usar o pi = 180 da trigononometria, ou a constante pi = 3,1415... em questões desse tipo??? Espero que entendam o q escrevi, Agradeço qualquer ajuda.
-
Kabection
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jan 16, 2012 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por emsbp » Ter Abr 17, 2012 13:18
por emsbp » Ter Abr 17, 2012 13:18
Boa tarde.
De facto, o desenvolvimento da tua resolução está correto.
Deves usar

como 180º quando aplicas diretamente em funções trigonométricas, ou seja, nos cálculos de sen, cos, tg, cotg, .... Portanto quanto calculas f(

), vais calcular o sen e cos de

, e logo, ao usares graus contará como 180º e se usares radianos contará como

.Tens de teres isto em atenção se usares a calculadora gráfica (averigua no MODE da máquina).
Agora, quando fores calcular o valor de
b (ordenada na origem da equação reduzida da tangente ao ponto dado), deves usar o valor real de

=3.14...., pois neste caso não estás a usar funções trigonométricas.
Espero ter ajudado.
Bom trabalho!
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Confusão com limite
por Kabection » Sex Mar 23, 2012 23:04
- 3 Respostas
- 1415 Exibições
- Última mensagem por LuizAquino

Sáb Mar 24, 2012 02:36
Cálculo: Limites, Derivadas e Integrais
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8842 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2265 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7486 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4965 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
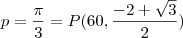 ------------- f(p)=
------------- f(p)=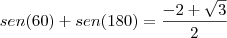

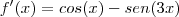
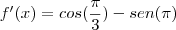
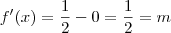

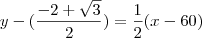


 , onde
, onde 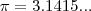 Então devo usar o pi = 180 da trigononometria, ou a constante pi = 3,1415... em questões desse tipo??? Espero que entendam o q escrevi, Agradeço qualquer ajuda.
Então devo usar o pi = 180 da trigononometria, ou a constante pi = 3,1415... em questões desse tipo??? Espero que entendam o q escrevi, Agradeço qualquer ajuda.

 como 180º quando aplicas diretamente em funções trigonométricas, ou seja, nos cálculos de sen, cos, tg, cotg, .... Portanto quanto calculas f(
como 180º quando aplicas diretamente em funções trigonométricas, ou seja, nos cálculos de sen, cos, tg, cotg, .... Portanto quanto calculas f( ), vais calcular o sen e cos de
), vais calcular o sen e cos de 





