Caiu a seguinte questão na minha prova de Cálculo I:
"Considere o polinômio de grau n, onde n é ímpar, dado por:
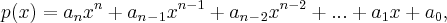
e os a são todos reais. Mostre, usando a teoria de limites, que p(x) admite pelo menos uma raiz real."
Daí eu respondi exatamente assim:
Toda função polinomial é contínua. E de acordo com o Teorema de Bolzano, em um intervalo [a,b] se f(a) e f(b) tiverem sinais contrários, então haverá pelo menos um c em que f(c) = 0.
Pela correção do professor, ele circulou o "f(a)" e o "f(b)" e escreveu "Isso ocorre no polinômio dado?" E a questão foi zerada.
Minha dúvida então é se eu errei por colocar f em vez de p, ou se ela é resolvida corretamente de outra forma.
Desde já agradeço!


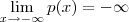 enquanto
enquanto 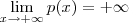 , logo existem pontos
, logo existem pontos 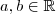 tais que
tais que 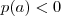 e
e 



 .
.



