 por Yumi » Qui Abr 12, 2012 18:23
por Yumi » Qui Abr 12, 2012 18:23
Já tentei de tudo mas não chego em nenhuma resposta... Meu cérebro vai fundir!!! Alguém me ajude por favor. Qualquer dica é bem vinda...
Um certo tipo de vírus tem um diâmetro de 0,02 x 10 elevado a três mm. Admita que uma colônia desses vírus pudesse ocupar totalmente uma superfície plana de 1 cm quadrado de área, numa única camada. Qual é o número máximo de indivíduos dessa colônia?
A - 4 x 10 elevado a seis
B - 25 x 10 elevado a seis
C - 25 x 10 elevado a dez
D - 25 x 10 elevado a doze
E - 50 x 10 elevado a doze
-
Yumi
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 12, 2012 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: cursando
 por MarceloFantini » Qui Abr 12, 2012 19:28
por MarceloFantini » Qui Abr 12, 2012 19:28
Yumi, por favor leia as regras do fórum, em especial a número 2. Use LaTeX para redigir suas fórmulas.
Sobre a questão, sabendo o diâmetro podemos calcular o raio, logo

. A área ocupada pelo vírus portanto é
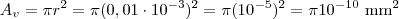
.
Para encontrar o número de vírus que cabem na área, divida o total coberto pela área de cada um e arredonde. Termine.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Yumi » Qui Abr 12, 2012 20:51
por Yumi » Qui Abr 12, 2012 20:51
MarceloFantini escreveu:Yumi, por favor leia as regras do fórum, em especial a número 2. Use LaTeX para redigir suas fórmulas.
Sobre a questão, sabendo o diâmetro podemos calcular o raio, logo

. A área ocupada pelo vírus portanto é
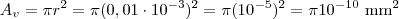
.
Para encontrar o número de vírus que cabem na área, divida o total coberto pela área de cada um e arredonde. Termine.
Me desculpe.
Minha nossa... fiquei ainda mais perdida...
-
Yumi
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 12, 2012 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Pedagogia
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- notação cientifica
por jose henrique » Qui Fev 10, 2011 22:45
- 1 Respostas
- 2494 Exibições
- Última mensagem por Molina

Sex Fev 11, 2011 02:16
Álgebra Elementar
-
- notação científica
por dandara » Dom Abr 24, 2016 11:32
- 1 Respostas
- 2783 Exibições
- Última mensagem por DanielFerreira

Dom Abr 24, 2016 14:18
Aritmética
-
- notação cientifica
por ezidia51 » Ter Mar 13, 2018 12:33
- 4 Respostas
- 3698 Exibições
- Última mensagem por ezidia51

Ter Mar 13, 2018 22:58
Números Complexos
-
- Questão de notação científica!
por LuizCarlos » Dom Out 23, 2011 17:44
- 1 Respostas
- 1965 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:15
Álgebra Elementar
-
- Notação Científica e Potenciação
por Bielto » Sáb Jul 28, 2012 10:35
- 4 Respostas
- 3920 Exibições
- Última mensagem por LuizAquino

Sáb Jul 28, 2012 14:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . A área ocupada pelo vírus portanto é
. A área ocupada pelo vírus portanto é 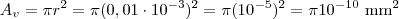 .
.

