A minha professora de GE pediu para que provássemos um teorema . Esse teorema é do primeiro capítulo de geometria plana , que diz o seguinte :
a) Se P e Q estão em lados opostos de uma reta r , e Q e T estão em lados opostos de r , então P e T estão do mesmo lado de r .
b) Se P e Q estão em lados opostos de uma reta r , e Q e T estão no mesmo lado de r , então P e T estão em lados opostos de r .
Eu tentei fazer da sequinte forma considera a hipótese e negar a tese e chegar numa conclusão por absurdo .
Mas eu acho que isso não é uma proposição simples do tipo
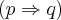 .
. Eu acho que é desse tipo
 .
.a) Se P e Q estão em lados opostos de uma reta r , e Q e T estão em lados opostos de r , então P e T não estão do mesmo lado r .
Só que eu estou perdido , eu não consigo formalizar o meu raciocínio. E por isso pesso a ajuda de voçês !


 um plano qualquer. Traçando uma reta qualquer, dividiremos esse plano em dois semiplanos. Agora, trataremos os planos como conjuntos de pontos, onde cada ponto que forma o plano é um elemento diferente. Os semiplanos A e B e a reta R são conjuntos de pontos, onde:
um plano qualquer. Traçando uma reta qualquer, dividiremos esse plano em dois semiplanos. Agora, trataremos os planos como conjuntos de pontos, onde cada ponto que forma o plano é um elemento diferente. Os semiplanos A e B e a reta R são conjuntos de pontos, onde: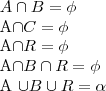
 . Esse absurdo prova a sentença.
. Esse absurdo prova a sentença.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.