 por Joseaugusto » Seg Abr 09, 2012 10:43
por Joseaugusto » Seg Abr 09, 2012 10:43
Olá amigos, travei com esses dois exercicios de complexos, e não encontro resolução na internet. Agradeceria a quem me indicar o caminho a ser seguido para resolve-los
(UFU) A soma das raizes distintas da equação z² + 2R(z) + 1 = 0, onde z é um numero complexo e R(z) denota a parte real de Z é igual a:
R: -1
(ITA) Sejam x e y numeros reais, com x =/= 0 (x diferente de zero), satisfazendo (x + iy)² = (x +y)i. Então:
R: x é raiz da equação x³ + 3x² + 2x - 6
-
Joseaugusto
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 06, 2012 11:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Seg Abr 09, 2012 18:46
por fraol » Seg Abr 09, 2012 18:46
(1)

Seja

, com

, então
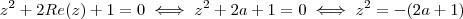
Note que
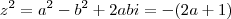
não possui parte imaginária donde concluímos que
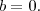
Assim
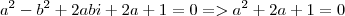
, de onde sai

( raiz dupla ).
Portanto a soma das raízes distintas é igual a -1.
(2)
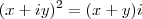

, note que no segundo membro não temos parte real, então

.
ou
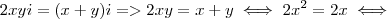
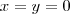
ou

.
Como

então

(que é a raiz real do polinômio dado).
(Obs. o ideal é que se crie um tópico para cada questão no forum.)
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Joseaugusto » Ter Abr 10, 2012 09:47
por Joseaugusto » Ter Abr 10, 2012 09:47
Sou implicado com complexos por causa disso, os exercícios são fáceis... depois que voce aprende como faze-los

obrigado pela ajuda fraol, coloquei as duas questões em um unico post pra não encher demais o forum, na próxima eu faço certo.
-
Joseaugusto
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Mar 06, 2012 11:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Ter Abr 10, 2012 10:35
por fraol » Ter Abr 10, 2012 10:35
Há matemáticos que dizem que os complexos só o são no nome. Valeu.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duas questões
por caio123 » Qua Ago 24, 2011 20:22
- 0 Respostas
- 1581 Exibições
- Última mensagem por caio123

Qua Ago 24, 2011 20:22
Logaritmos
-
- Duas questões de Geometria.
por JoaoGabriel » Dom Set 26, 2010 09:34
- 4 Respostas
- 7852 Exibições
- Última mensagem por JoaoGabriel

Dom Set 26, 2010 14:49
Geometria Plana
-
- Quádricas - Duas questões
por renan_a » Seg Jan 21, 2013 00:13
- 2 Respostas
- 5147 Exibições
- Última mensagem por renan_a

Qui Fev 07, 2013 08:43
Geometria Analítica
-
- Dúvidas com essas duas questões.
por Dimas » Qui Dez 09, 2010 12:42
- 0 Respostas
- 1460 Exibições
- Última mensagem por Dimas

Qui Dez 09, 2010 12:42
Binômio de Newton
-
- [Logaritmo] duas questões para resolução com urgência
por Cristian Cristiano » Qua Mai 03, 2017 04:37
- 0 Respostas
- 4052 Exibições
- Última mensagem por Cristian Cristiano

Qua Mai 03, 2017 04:37
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 , com
, com  , então
, então 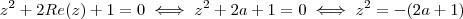
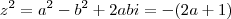 não possui parte imaginária donde concluímos que
não possui parte imaginária donde concluímos que 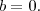
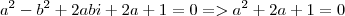 , de onde sai
, de onde sai  ( raiz dupla ).
( raiz dupla ).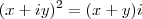
 , note que no segundo membro não temos parte real, então
, note que no segundo membro não temos parte real, então .
.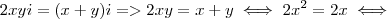
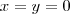 ou
ou  .
.  então
então (que é a raiz real do polinômio dado).
(que é a raiz real do polinômio dado).
