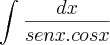
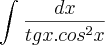
Considerando tgx = u, teremos dx = du.cos²x:
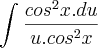
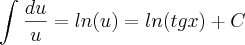
Posso resolver dessa forma ?? Se estiver errado, por favor, façam da forma correta.

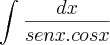
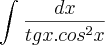
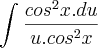
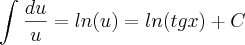


nietzsche escreveu:Considerando tgx = u, teremos dx = du.cos²x" : Se u=sex/cos x, então du/dx ? cos²x.

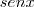 e
e 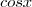 pela diferença dos logaritmos.
pela diferença dos logaritmos.
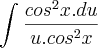

 be an interval and g : [a,b]
be an interval and g : [a,b]  I be a continuously differentiable function. Suppose that f : I
I be a continuously differentiable function. Suppose that f : I is a continuous function. Then
is a continuous function. Then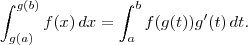

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.
 :
: