 por Raphaela_sf » Qui Abr 05, 2012 19:11
por Raphaela_sf » Qui Abr 05, 2012 19:11
Boa tarde,
Tenho dúvidas sobre a forma numérica (intuitiva) de encontrar um limite e a forma lim f(x) para x --> a = f(a).
Sendo o valor numérico, impreciso, ocasionando erros, faz-se necessário o uso de 'ferramentas algébricas'.
Para o exemplo, f(x) = (x² + 4x) para x-->2. Sei que o limite é igual a 12 apenas pelo cálculo de f(2). Se há uma indeterminação só posso realizar este processo quando simplificada a equação. Existe alguma outra situação que me impeça de utilizar esse meio, ou mesmo a forma intuitiva com os limites laterais?
Muito Obrigada!
-
Raphaela_sf
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 05, 2012 18:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por LuizAquino » Qui Abr 05, 2012 20:56
por LuizAquino » Qui Abr 05, 2012 20:56
Raphaela_sf escreveu:Tenho dúvidas sobre a forma numérica (intuitiva) de encontrar um limite e a forma lim f(x) para x --> a = f(a).
Sendo o valor numérico, impreciso, ocasionando erros, faz-se necessário o uso de 'ferramentas algébricas'.
Para o exemplo, f(x) = (x² + 4x) para x-->2. Sei que o limite é igual a 12 apenas pelo cálculo de f(2). Se há uma indeterminação só posso realizar este processo quando simplificada a equação. Existe alguma outra situação que me impeça de utilizar esse meio, ou mesmo a forma intuitiva com os limites laterais?
Não existe. Sempre podemos aplicar uma das estratégias: numérica; algébrica. Lembrando que a estratégia algébrica é preferível, pois a numérica é imprecisa.
Além disso, vale lembrar que você não "
simplifica a equação". Não há uma
equação. O que há é uma
função, que você tenta simplificar a sua
expressão toda vez que no limite aparece uma indeterminação.
Por exemplo, considere a função

. Ao tentar calcular

, temos uma indeterminação do tipo 0/0.
Podemos então efetuar a seguinte simplificação:

Note que agora no limite há uma outra função, que seria por exemplo g(x) = x + 1. Não aparece mais a função f(x) original. Entretanto, por esse desenvolvimento podemos dizer que:

Mas como a função g é contínua (você ainda deve estudar o conceito de continuidade), podemos dizer que

.
Conclusão:
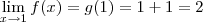
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Raphaela_sf » Sex Abr 06, 2012 13:29
por Raphaela_sf » Sex Abr 06, 2012 13:29
Desculpe, mas a noção de continuidade me parece vaga.
Como saber se uma função é contínua?
Sei que quando
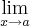
f(x) = f(a), essa função é contínua em
a.
Porque, como você disse g(x) é contínua e por isso se pode aplicar a definição algébrica de limite.
Isto é, g(x) = x+1, você verificou a função, a classificou como contínua e aplicou a definição.
Ou estou entendendo errado?
Muito Obrigada mesmo!
-
Raphaela_sf
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Abr 05, 2012 18:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Ambiental
- Andamento: cursando
 por LuizAquino » Sex Abr 06, 2012 19:17
por LuizAquino » Sex Abr 06, 2012 19:17
Raphaela_sf escreveu:Desculpe, mas a noção de continuidade me parece vaga.
Como saber se uma função é contínua?
Sei que quando
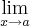
f(x) = f(a), essa função é contínua em
a.
Eu recomendo que você assista a videoaula "04. Cálculo I - Limites e Continuidade". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquinoSe após assistir essa videoaula a dúvida continuar, então poste aqui novamente.
Raphaela_sf escreveu:Porque, como você disse g(x) é contínua e por isso se pode aplicar a definição algébrica de limite.
O que você está chamando de "definição algébrica" de limite? Por acaso seria:
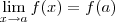
? Isso não é a "definição algébrica" de limite. Na verdade, como você mesmo já disse acima, isso aparece na definição de continuidade de f no ponto x = a.
Raphaela_sf escreveu:Isto é, g(x) = x+1, você verificou a função, a classificou como contínua e aplicou a definição.
Ou estou entendendo errado?
Está correto. Ao verificar que g(x) é contínua, podemos aplicar a definição de continuidade e escrever por exemplo que:

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- conceito de integral e limite
por OtavioBonassi » Sex Jan 07, 2011 15:52
- 11 Respostas
- 8668 Exibições
- Última mensagem por OtavioBonassi

Dom Jan 09, 2011 22:47
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Conceito de Existência
por eli83 » Qua Out 10, 2012 10:33
- 4 Respostas
- 2564 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 17:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6641 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4786 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5117 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 . Ao tentar calcular
. Ao tentar calcular  , temos uma indeterminação do tipo 0/0.
, temos uma indeterminação do tipo 0/0.

 .
.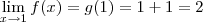

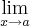 f(x) = f(a), essa função é contínua em
f(x) = f(a), essa função é contínua em 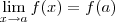 ? Isso não é a "definição algébrica" de limite. Na verdade, como você mesmo já disse acima, isso aparece na definição de continuidade de f no ponto x = a.
? Isso não é a "definição algébrica" de limite. Na verdade, como você mesmo já disse acima, isso aparece na definição de continuidade de f no ponto x = a.




