Raphaela_sf escreveu:Tenho dúvidas sobre a forma numérica (intuitiva) de encontrar um limite e a forma lim f(x) para x --> a = f(a).
Sendo o valor numérico, impreciso, ocasionando erros, faz-se necessário o uso de 'ferramentas algébricas'.
Para o exemplo, f(x) = (x² + 4x) para x-->2. Sei que o limite é igual a 12 apenas pelo cálculo de f(2). Se há uma indeterminação só posso realizar este processo quando simplificada a equação. Existe alguma outra situação que me impeça de utilizar esse meio, ou mesmo a forma intuitiva com os limites laterais?
Não existe. Sempre podemos aplicar uma das estratégias: numérica; algébrica. Lembrando que a estratégia algébrica é preferível, pois a numérica é imprecisa.
Além disso, vale lembrar que você não "
simplifica a equação". Não há uma
equação. O que há é uma
função, que você tenta simplificar a sua
expressão toda vez que no limite aparece uma indeterminação.
Por exemplo, considere a função

. Ao tentar calcular

, temos uma indeterminação do tipo 0/0.
Podemos então efetuar a seguinte simplificação:

Note que agora no limite há uma outra função, que seria por exemplo g(x) = x + 1. Não aparece mais a função f(x) original. Entretanto, por esse desenvolvimento podemos dizer que:

Mas como a função g é contínua (você ainda deve estudar o conceito de continuidade), podemos dizer que

.
Conclusão:
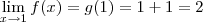


 . Ao tentar calcular
. Ao tentar calcular  , temos uma indeterminação do tipo 0/0.
, temos uma indeterminação do tipo 0/0.

 .
.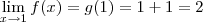

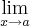 f(x) = f(a), essa função é contínua em
f(x) = f(a), essa função é contínua em 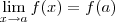 ? Isso não é a "definição algébrica" de limite. Na verdade, como você mesmo já disse acima, isso aparece na definição de continuidade de f no ponto x = a.
? Isso não é a "definição algébrica" de limite. Na verdade, como você mesmo já disse acima, isso aparece na definição de continuidade de f no ponto x = a. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.