Mostre que os pontos (0,1,-1), (1,3,0) e (2,5,1) são colineares.
Também não consegui resolver esse exercício, fiz um com dois pontos, ai fiz uma relação de proporcionalidade entre os pontos e deu certo.
Agora com os três pontos não deu certo.



 tal que:
tal que: .(vetor BC)
.(vetor BC) .(1,2,1)
.(1,2,1) =1
=1
Lucio Carvalho escreveu:os vetores AB e BC (nota: falta a seta)
[tex]\vec{AB}[/tex]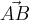
[tex]\overrightarrow{AB}[/tex]
 . Já a Forma 2) é mais interessante de ser usada quando temos duas letras em maiúsculo:
. Já a Forma 2) é mais interessante de ser usada quando temos duas letras em maiúsculo:  .
.

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.