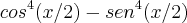 É IGUAL A:
É IGUAL A:PS: NÃO TENHO A MÍNIMA NOÇÃO DO QUE FAZER! AGRADEÇO A AJUDA DESDE JÁ!

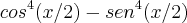 É IGUAL A:
É IGUAL A:
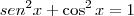 ; segundo, o cosseno do arco duplo
; segundo, o cosseno do arco duplo  ; por último, a fatoração de diferença de potências à quarta
; por último, a fatoração de diferença de potências à quarta 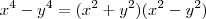 . Tente usar estes fatos para a resolução do exercício.
. Tente usar estes fatos para a resolução do exercício.

MarceloFantini escreveu:Vou lembrar algumas relações trigonométricas importantes: primeiro, a relação fundamental; segundo, o cosseno do arco duplo
; por último, a fatoração de diferença de potências à quarta
. Tente usar estes fatos para a resolução do exercício.
 e
e  está correto ultlizar essa informação nessa equação?
está correto ultlizar essa informação nessa equação?
\cos^2 \left( \frac{x}{2} \right) = \frac{1 + \cos x}{2}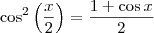 . Sim, elas são válidas, porém não levarão à resolução mais rápida do exercício. Além disso, elas são consequência das duas primeiras relações que escrevi.
. Sim, elas são válidas, porém não levarão à resolução mais rápida do exercício. Além disso, elas são consequência das duas primeiras relações que escrevi.



MarceloFantini escreveu:Por favor, procure escrever tudo corretamente no LaTeX. O código éque sai
- Código: Selecionar todos
\cos^2 \left( \frac{x}{2} \right) = \frac{1 + \cos x}{2}. Sim, elas são válidas, porém não levarão à resolução mais rápida do exercício. Além disso, elas são consequência das duas primeiras relações que escrevi.
Façamos isso passo a passo. Primeiro, escreva a fatoração das potências à quarta na expressão dada.
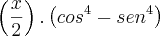
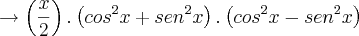
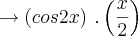

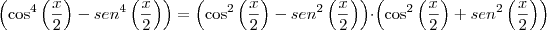 .
.

MarceloFantini escreveu:Não tenha pressa. Sua fatoração não está correta. O caminho certo é.
Agora, o que você pode dizer do fator direito e do fator esquerdo no produto?
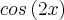 E O FATOR DIREITO É A RELAÇÃO FUNDAMENTAL EQUIVALENTE A
E O FATOR DIREITO É A RELAÇÃO FUNDAMENTAL EQUIVALENTE A  ESTÁ CORRETO?
ESTÁ CORRETO?
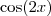 mas sim
mas sim  . O arco é
. O arco é  e não apenas
e não apenas  .
.

MarceloFantini escreveu:O fator direito está certo, o esquerdo não. Não serámas sim
. O arco é
e não apenas
.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)