Estou resolvendo alguns exercícios de equações, e fiquei em dúvida!
O exercício pede para encontrar duas equações equivalentes a cada equação dada! resolvi algumas e consegui encontrar duas equações equivalentes, mas na ultima questão, não entendi.
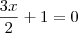
Resolvi a equação:
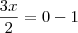
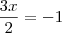


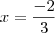
Esse resultado é equivalente :
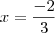
Mas agora buscando a segunda equação que seja equivalente:
Adicionando 2 a cada termo nos dois membros da equação!
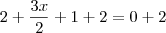
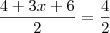



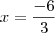

Mas agora multiplicando 2 por cada termo nos dois membros da equação!
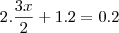
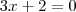
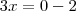

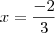
Essa equação
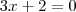 é equivalente a
é equivalente a 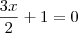
Por que , com o princípio aditivo da igualdade, somando 2 a cada termo dos dois membros da equação, não obtive o resultado
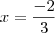


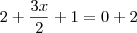 , e não
, e não 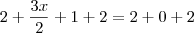 . Note que você somou 4 do lado esquerdo e 2 do lado direito, que gerou uma equação diferente e chegou ao resultado errado.
. Note que você somou 4 do lado esquerdo e 2 do lado direito, que gerou uma equação diferente e chegou ao resultado errado.

