valha.Dê então um valor pra
>0 tal que para todo x satisfazendo 0<|x-a|< a desigualdade |f(x)-L|<seja verdadeira.f(x)=
, L=3, a=10, =1o intervalo eu conseguir achar, da seguinte maneira:
0<|x-10|<
|-3|<13-1<|
<42<|
<44<|19-x|<16
-15<|-x|<-3
15>|x|>3
logo (3,15) confere com a resposta do livro, acredito que a resolução esteja correta.
Mas ai, o valor de
não consigo achar, sempre acho -7, mas no livro a resposta é 5.Alguem poderia ajudar-me por favor?
Obg
Ps: Livro Calculo 1, Thomas, pag 92, nro 19
dado, você encontrou 
.
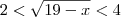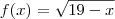, encontramos 
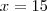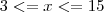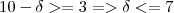e 
.
.
e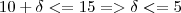
a implicação do limite será satisfeita.
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.