 por samra » Sáb Mar 31, 2012 02:38
por samra » Sáb Mar 31, 2012 02:38
Ei gente, nn estou conseguindo resolver este limite, qlq forma que eu uso dá indeterminação

Ajuda pf?
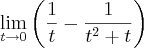
Ai eu tento resolver assim, mas nn to conseguindo sair do lugar =/


?????????????????????
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por LuizAquino » Sáb Mar 31, 2012 12:11
por LuizAquino » Sáb Mar 31, 2012 12:11
samra escreveu: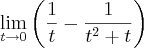
Ai eu tento resolver assim, mas nn to conseguindo sair do lugar =/
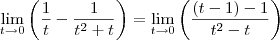
Você errou já no primeiro passo.
Você precisa subtrair duas frações, sendo que os seus denominadores são t e t² + t.
No segundo denominador, colocando t em evidência, obtemos t(t + 1).
Devemos então determinar o m. m. c. entre t e t(t + 1). Acontece que o m. m. c. entre essas duas expressões é t(t + 1).
Desse modo, o primeiro passo na resolução do limite será:
![\lim_{t\to 0}\left(\frac{1}{t}-\frac{1}{{t}^{2}+t} \right) = \lim_{t\to 0}\left[\frac{(t + 1) - 1}{t(t + 1)}\right] \lim_{t\to 0}\left(\frac{1}{t}-\frac{1}{{t}^{2}+t} \right) = \lim_{t\to 0}\left[\frac{(t + 1) - 1}{t(t + 1)}\right]](/latexrender/pictures/99539b8e5d97bf217e2c7e2f12b2221a.png)
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por samra » Dom Abr 01, 2012 12:34
por samra » Dom Abr 01, 2012 12:34
Editado pela última vez por
samra em Dom Abr 01, 2012 12:41, em um total de 2 vezes.
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por samra » Dom Abr 01, 2012 12:40
por samra » Dom Abr 01, 2012 12:40
Eu tentei resolvê-lo aki, só não sei se está certo:

Não sei se está certo, até pq o livro nn tras a resposta do mesmo.
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por fraol » Dom Abr 01, 2012 14:56
por fraol » Dom Abr 01, 2012 14:56
O valor 1 para o limite está certo.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como resolver esse limite?
por duborgis » Sex Abr 06, 2012 13:29
- 12 Respostas
- 7764 Exibições
- Última mensagem por Fabio Wanderley

Dom Abr 08, 2012 16:04
Cálculo: Limites, Derivadas e Integrais
-
- como resolver esse limite
por mayconf » Dom Set 23, 2012 01:31
- 4 Respostas
- 2621 Exibições
- Última mensagem por mayconf

Seg Set 24, 2012 02:50
Cálculo: Limites, Derivadas e Integrais
-
- Como resolver esse problema?
por denfo » Sex Dez 04, 2009 13:22
- 1 Respostas
- 6616 Exibições
- Última mensagem por denfo

Qui Dez 10, 2009 20:16
Matemática Financeira
-
- Não sei como começar a resolver esse problema
por Sil » Ter Nov 02, 2010 19:36
- 5 Respostas
- 6256 Exibições
- Última mensagem por Sil

Ter Nov 02, 2010 21:40
Matemática Financeira
-
- como resolver esse tipo de conta?
por LuizCarlos » Seg Jul 11, 2011 00:43
- 11 Respostas
- 6170 Exibições
- Última mensagem por LuizCarlos

Ter Jul 12, 2011 20:00
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
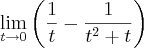



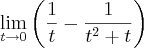



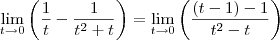
![\lim_{t\to 0}\left(\frac{1}{t}-\frac{1}{{t}^{2}+t} \right) = \lim_{t\to 0}\left[\frac{(t + 1) - 1}{t(t + 1)}\right] \lim_{t\to 0}\left(\frac{1}{t}-\frac{1}{{t}^{2}+t} \right) = \lim_{t\to 0}\left[\frac{(t + 1) - 1}{t(t + 1)}\right]](/latexrender/pictures/99539b8e5d97bf217e2c7e2f12b2221a.png)






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.