Área destinada para assuntos gerais ou considerados off-topic, excluindo quaisquer propagandas comerciais ou anúncios.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Cleyson007 » Sáb Mar 31, 2012 16:14
por Cleyson007 » Sáb Mar 31, 2012 16:14
Boa tarde a todos!
Na verdade, estou precisando que alguém me dê uma mãozinha com LaTeX..
Estou estudando integrais iteradas e estou encontrando dificuldade de montar minha resolução usando o editor de LaTeX.
A questão é a seguinte: Ao resolver a parte interna da integral colocando a antiderivada, como faço para colocar o intervalo de integração através do LaTeX (aquela barra vertical com o intervalo).
Se alguém souber e puder me ajudar ficarei agradecido..
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por DanielFerreira » Sáb Mar 31, 2012 17:02
por DanielFerreira » Sáb Mar 31, 2012 17:02
Cleyson,
utilize o "editor de fórmulas" que fica na barra (B, i, ... tex, editor de fórmulas)
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Cleyson007 » Sáb Mar 31, 2012 17:06
por Cleyson007 » Sáb Mar 31, 2012 17:06
Boa tarde Danjr!
Danjr, eu sei que existe o botão Editor de Fórmulas eu não sei o comando que devo utilizar para representar o intervalo da antiderivada (aquela barra na vertical).
Pode me ajudar?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por DanielFerreira » Sáb Mar 31, 2012 17:16
por DanielFerreira » Sáb Mar 31, 2012 17:16
Seria
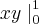
ou
![\int_{1}^{3}
\left[xy \right]_{0}^{1}dx \int_{1}^{3}
\left[xy \right]_{0}^{1}dx](/latexrender/pictures/e596921f27a68e671b1da8aa7f01acff.png)
ou
nenhum deles?
rsrs
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Cleyson007 » Sáb Mar 31, 2012 17:24
por Cleyson007 » Sáb Mar 31, 2012 17:24
Boa tarde Danjr!
Danjr, seria o primeiro exemplo mesmo rsrsrs..
Só que o exemplo que você me passou o intervalo é de 0 a 1.. Se envolvesse raiz o espaço fica pequeno demais. Veja o exemplo:
![yx\left \right|_{-\,\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}} yx\left \right|_{-\,\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}}](/latexrender/pictures/4da66e5ff8c81d8056e51876931633b0.png)
Existe uma maneira de corrigir?
Outra dúvida: Qual o botão você utilizou para chegar em \left \right|_{}^{} ?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por DanielFerreira » Sáb Mar 31, 2012 17:45
por DanielFerreira » Sáb Mar 31, 2012 17:45
Cleyson007 escreveu:Outra dúvida: Qual o botão você utilizou para chegar em \left \right|_{}^{} ?
Até mais.
Aquelas barras depois dos parênteses, eu apaguei a primeira.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Assuntos Gerais ou OFF-TOPIC
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LaTeX
por Sacadelae » Qua Dez 09, 2015 02:35
- 0 Respostas
- 18251 Exibições
- Última mensagem por Sacadelae

Qua Dez 09, 2015 02:35
Álgebra Elementar
-
- LaTeX
por Sacadelae » Qua Dez 09, 2015 02:36
- 0 Respostas
- 17128 Exibições
- Última mensagem por Sacadelae

Qua Dez 09, 2015 02:36
Álgebra Elementar
-
- problemas no editor latex
por adauto martins » Qui Jan 28, 2016 10:13
- 2 Respostas
- 3201 Exibições
- Última mensagem por adauto martins

Sex Jan 29, 2016 09:42
Álgebra Elementar
-
- Obter o comando LaTeX para algum símbolo
por LuizAquino » Seg Abr 11, 2011 19:24
- 1 Respostas
- 5779 Exibições
- Última mensagem por Neperiano

Sex Out 21, 2011 16:28
Sites Recomendados / Outras Indicações
-
- [Dúvida ANOVA] Uma dúvida sobre a estatística correta
por gustamfar » Ter Mai 22, 2018 18:19
- 0 Respostas
- 11051 Exibições
- Última mensagem por gustamfar

Ter Mai 22, 2018 18:19
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




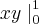
![\int_{1}^{3}
\left[xy \right]_{0}^{1}dx \int_{1}^{3}
\left[xy \right]_{0}^{1}dx](/latexrender/pictures/e596921f27a68e671b1da8aa7f01acff.png)
![yx\left \right|_{-\,\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}} yx\left \right|_{-\,\sqrt[]{4-2{y}^{2}}}^{\sqrt[]{4-2{y}^{2}}}](/latexrender/pictures/4da66e5ff8c81d8056e51876931633b0.png)

 .
.
 :
: