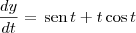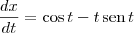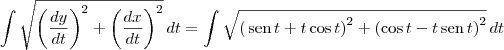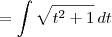Essa questão caiu na minha prova de Calculo, ontem. Por favor me dêem uma ajuda pra entender.
Encontre o cumprimento da curva:
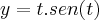
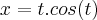
nos limites
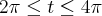 .
.Fiz da seguinte forma:
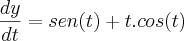 pela regra do produto (derivação)
pela regra do produto (derivação)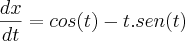
Aplicando na equação de comprimento da curva:
![\int_{}^{}\sqrt[]{\left(\frac{dy}{dt} \right)^2+\left(\frac{dx}{dt} \right)^2 dt} \int_{}^{}\sqrt[]{\left(\frac{dy}{dt} \right)^2+\left(\frac{dx}{dt} \right)^2 dt}](/latexrender/pictures/33cc0036a6033b6fe14d2241a6023406.png)
Onde por regra o resultado seria:
![\int_{}^{}\sqrt[]{a^2+u^2}du= \frac{u}{2}\sqrt[]{a^2+u^2}+\frac{a^2}{2}ln\left|u+\sqrt[]{a^2+u^2} \right|+C \int_{}^{}\sqrt[]{a^2+u^2}du= \frac{u}{2}\sqrt[]{a^2+u^2}+\frac{a^2}{2}ln\left|u+\sqrt[]{a^2+u^2} \right|+C](/latexrender/pictures/387f025849ea579d1d1e26d665e9978a.png)
![\frac{cos(t)-t.sen(t)}{2}.\sqrt[]{\left(sen^2t + t^2.cos^2t \right)+ \left(cos^2t + t^2sen^2t \right)} + \frac{sen^2t + t^2cos^2t}{2} \frac{cos(t)-t.sen(t)}{2}.\sqrt[]{\left(sen^2t + t^2.cos^2t \right)+ \left(cos^2t + t^2sen^2t \right)} + \frac{sen^2t + t^2cos^2t}{2}](/latexrender/pictures/1a1be7513ef0d83039cb78065af8230c.png) .
. ![ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C](/latexrender/pictures/cbd1afafce59129efed1a9d11c1e8acc.png)
Pra tentar organizar, fiz o seguinte:
OBS:
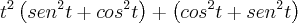
Ficou:
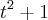
Voltando:
![\frac{cos(t)-tsen(t)}{2}.\sqrt[]{t^2+1^2} + \frac{sen^2(t) + t^2cos^2(t)}{2}ln\left|cos(t)-tsen(t)+\sqrt[]{ t^2+1^2} \right| \frac{cos(t)-tsen(t)}{2}.\sqrt[]{t^2+1^2} + \frac{sen^2(t) + t^2cos^2(t)}{2}ln\left|cos(t)-tsen(t)+\sqrt[]{ t^2+1^2} \right|](/latexrender/pictures/2beace109dd7d611f7eba901669eb66c.png)
Este é o caminho? Ja continuo...


![\, . \, ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C \, . \, ln\left|\left(cos(t)-tsen(t) \right) +\sqrt[]{\left(sen^2t+t^2cos^2t \right)+\left(cos^2t +t^2sen^2t \right)}\right|+C](/latexrender/pictures/48e1160bd21aa4fbbb0aff3110057ade.png)
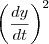 é uma constante. Esse não é o caso, já que esse termo é dependente da variável da integral (que no caso é
é uma constante. Esse não é o caso, já que esse termo é dependente da variável da integral (que no caso é