por cjunior94 » Dom Mar 25, 2012 22:54
![\lim_{x->3} \frac{-1*(3-x)*\pi}{\pi*sen[\pi*(3-x)]}](/latexrender/pictures/3f2f4fc398a372cc58275fbae109a921.png "\lim_{x->3} \frac{-1*(3-x)*\pi}{\pi*sen[\pi*(3-x)]}")
![sen(\pi*x)=Sen(3*\pi-\pi*x)=sen[\pi*(3-x)]](/latexrender/pictures/c720d5a3da75240c7d87fab88bebd33e.png "sen(\pi*x)=Sen(3*\pi-\pi*x)=sen[\pi*(3-x)]")
na fracão e também que foi colocado o -1 em evidencia, mas não consegui entender a afirmação que: 
por Fabio Wanderley » Seg Mar 26, 2012 00:55
cjunior94 escreveu:
Consegui perceber que ocorreu uma multiplicação por
por cjunior94 » Seg Mar 26, 2012 01:12
por LuizAquino » Seg Mar 26, 2012 01:21
cjunior94 escreveu:Mesmo após você falar que foi usada a formula de diferença de senos eu não consegui identificar o que foi realmente feito. Pode me explicar detalhadamente?
?
?
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
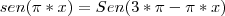
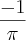
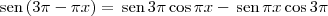
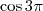![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)